积分放缩法

2011年高考数学四川卷理科数学第22题（压轴题）：

已知$f\left( x \right) = \dfrac{2}{3}x + \dfrac{1}{2}$，$h\left( x \right) = \sqrt x$．

（1）设函数$F(x)=f(x)-h(x)$，求$F(x)$的单调区间与极值；

（2）设$a\in\mathcal R$，解关于$x$的方程

$${\log_4}\left[\frac 32f(x-1)-\frac 34\right]={\log_2}h(a-x)-{\log_2}h(4-x);$$

（3）试比较$f\left( {100} \right)h\left( {100} \right) - \sum\limits_{k = 1}^{100} {h\left( k \right)}$与$\dfrac{1}{6}$的大小关系．

---

（1）解    函数$F(x)$的导函数

$$F'(x)=\dfrac{4\sqrt x-3}{6\sqrt x},x>0,$$ 于是$F(x)$的单调递减区间是$\left(0,\dfrac {9}{16}\right)$；$F(x)$单调递增区间是$\left(\dfrac{9}{16},+\infty\right)$．当$x=\dfrac{9}{16}$时，函数$F(x)$取得极小值$\dfrac 18$，函数$F(x)$没有极大值．

（2）解    原方程等价于

$$\dfrac 12{\log_2}(x-1)+{\log_2}\sqrt{4-x}={\log_2}\sqrt{a-x},$$ 即 $$\begin{cases} 1<x<4,\\ x<a,\\ a=-x^2+6x-4,\end{cases}$$ 画出函数$y=-x^2+6x-4$和$y=x$的图象，如图．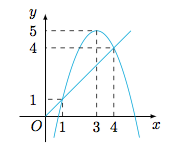
于是可得，当$1<a\leqslant 4$或$a=5$时，原方程有一解$x=3-\sqrt {5-a}$；$4<a<5$时，原方程有两解$x=3\pm\sqrt{5-a}$；当$a\leqslant 1$或$a>5$时，原方程无解．

（3）解    令

$$\begin{split}{S_n} &= f\left( n \right) \cdot g\left( n \right) - \sum\limits_{k = 1}^n {h\left( k \right)}\\&= \left( {\dfrac{2}{3}n + \dfrac{1}{2}} \right) \cdot \sqrt n - \sum\limits_{k = 1}^n {\sqrt k },\end{split}$$ 则 $${S_1} = \left( {\dfrac{2}{3} + \dfrac{1}{2}} \right) \cdot 1 - 1 = \dfrac{1}{6},$$ 事实上，有 $$\begin{split}{S_2} &= \left( {\dfrac{2}{3} \cdot 2 + \dfrac{1}{2}} \right) \cdot \sqrt 2 - 1 - \sqrt 2\\& = \dfrac{{5\sqrt 2 }}{6} - 1 \\&> \dfrac{7}{6} - 1 = \dfrac{1}{6},\end{split}$$

考虑证明${S_n}$单调递增．

$$\begin{split}{S_{n + 1}} - {S_n} &= \left[ {\dfrac{2}{3}\left( {n + 1} \right) + \dfrac{1}{2}} \right]\sqrt {n + 1} - \sum\limits_{k = 1}^{n + 1} {\sqrt k } - \left( {\dfrac{2}{3}n + \dfrac{1}{2}} \right)\sqrt n + \sum\limits_{k = 1}^n {\sqrt k } \\& = \left( {\dfrac{2}{3}n + \dfrac{1}{6}} \right)\sqrt {n + 1} - \left( {\dfrac{2}{3}n + \dfrac{1}{2}} \right)\sqrt n \\& = \dfrac{1}{6}\left[ {\left( {4n + 1} \right)\sqrt {n + 1} - \left( {4n + 3} \right)\sqrt n } \right]\\& = \dfrac{1}{6}\left( {\sqrt {16{n^3} + 24{n^2} + 9n + 1} - \sqrt {16{n^3} + 24{n^2} + 9n} } \right)\\& > 0,\end{split}$$ 因此当$n \geqslant 2$时，${S_n} > {S_1} = \dfrac{1}{6}$．

---

注    （3）的另解，利用加强的积分放缩，如图．

可得

$$\begin{split}&\qquad f(100)h(100)-\sum_{k=1}^{100}{h(k)}-\frac 16\\&=\frac{1343}{2}-\sum_{k=1}^{100}\sqrt k\\&>\frac{1343}{2}-\left[\int_{1}^{100}\sqrt x{\rm d}x+\frac 12\left(\sqrt{100}+1\right)\right]\\&=\frac{1343}{2}-\left[\frac 23\left( {100}^{1.5}-1\right)+\frac {11}2\right]\\&=0.\end{split}$$