每日一题[1035]双曲面

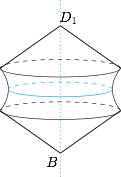
已知异面直线 $AB,CD$，求证：以 $AB$ 为轴将 $CD$ 旋转一周得到的曲面是双曲面（双曲面即双曲线绕其对称轴旋转生成的曲面，分单叶双曲面与双叶双曲面）．

---

分析与解　如图，设 $OH$ 是异面直线 $AB,CD$ 的公垂线段，并建立平面直角坐标系 $xOy$．$P$ 点为 $D$ 点在旋转一周的过程中在轴截面 $xOy$ 上的对应点．
设 $\overrightarrow{AB}$ 和 $\overrightarrow{CD}$ 的夹角为 $\theta$．由

$$\overrightarrow{BD}=\overrightarrow{BO}+\overrightarrow{OH}+\overrightarrow{HD},$$ 可得 $$BD^2=BO^2+OH^2+HD^2-2\cdot BO\cdot HD\cdot\cos\theta,$$ 又 $BO=HD\cdot\cos\theta$，且 $BD=BP$，于是 $$BP^2-\left(\dfrac{1}{\cos^2\theta}-1\right)BO^2=OH^2,$$ 也即 $$BP^2-\tan^2\theta\cdot BO^2=OH^2,$$ 此数量关系符合双曲线方程，因此命题得证．

---

给出一道与此相关的练习：

在正方体 $ABCD-A_1B_1C_1D_1$ 中，点 $P$ 在正方体表面运动，$P$不与$A$重合，如果 $S_{\triangle ABD_1}=S_{\triangle PBD_1}$，那么这样的点 $P$ 个数为______．

正确答案是$5$个．
根据题意，$P$ 点到正方体的体对角线 $BD_1$ 的距离与 $A$ 点到 $BD_1$ 的距离相同，因此 $P$ 点在以 $BD_1$ 为轴，$d(A,BD_1)$ 为半径的圆柱面上．
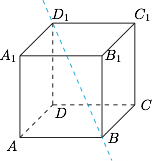如图，考虑到正方体绕直线 $BD_1$ 旋转形成的曲面由圆锥面和双曲面（异面直线绕其中一条旋转形成）构成，因此公共点共有 $5$ 个，为除 $A,B,D_1$ 以外的正方体的顶点．