每日一题[902]挖掘长度关系

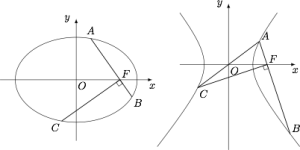
(1) 已知椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的右焦点为$F$，过$F$的直线交椭圆于$A,B$两点，点$C$是点$A$关于原点$O$的对称点，若$CF\perp AB$且$CF=AB$，则椭圆的离心率为_______；

(2) 已知双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$($a,b>0$)的右焦点为$F$，过$F$的直线交双曲线于$A,B$两点，点$C$是点$A$关于原点$O$的对称点，若$CF\perp AB$且$CF=FB$，则双曲线的离心率为_______．

---

正确答案是(1)$\sqrt 6-\sqrt 3$；(2)$\dfrac{\sqrt{10}}2$．

分析与解　先考虑(1)设左焦点为$F'$，$AF=x$，则直角$\triangle F'AB$的三边都可以用$a,x$表示，分别为

$$2a-x,2a-x,2x,$$ 于是有$2x=\sqrt 2(2a-x)$，解得$x=2a(\sqrt 2-1)$，从而有 $$4c^2=x^2+(2a-x)^2=4a^2\cdot(9-6\sqrt 2),$$ 得到离心率的值．

(2)与(1)类似，在直角$\triangle F'AB$中，有

$$(2a+x)^2+(2a+2x)^2=(4a+x)^2\Rightarrow x=a.$$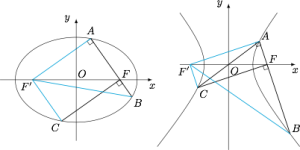

注　也可以利用焦点弦的调和平均性质列出方程组计算．