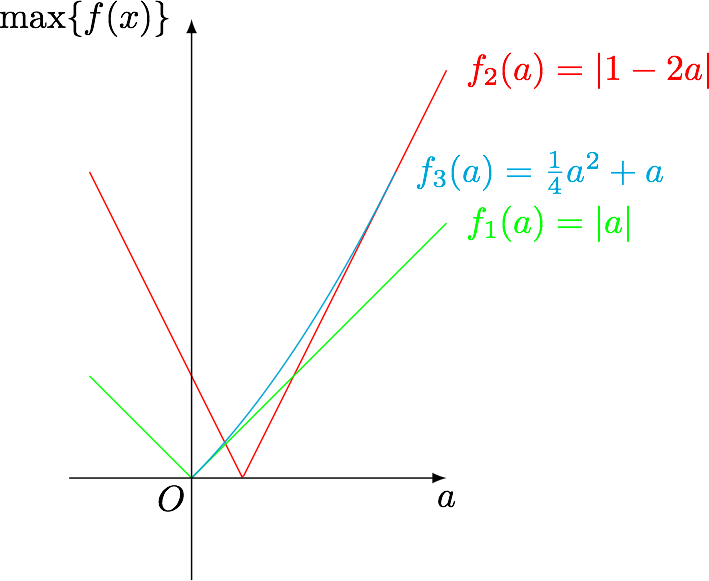每日一题[519]古原争霸

已知$g(x)=|x^2-ax-a|$，若对任意实数$a$，存在$x_0\in [0,1]$，使$g(x_0)\geqslant k$成立，求$k$的取值范围．

分析    显然问题的关键是求当参数$a$变化时，函数$g(x)$在$[0,1]$上的最大值的最小值．而函数$g(x)$在区间$[0,1]$上的函数值的最大值必然在两个端点和顶点（仅当$0\leqslant a\leqslant 2$时参与）竞争得到，画图规划即可．

解    在同一平面直角坐标系中画出$f_1(a)=|a|$，$f_2(a)=|1-2a|$和$f_3(a)=\dfrac 14a^2+a$($0\leqslant a \leqslant 2$)的图象，如图．

结合图形计算可得在函数$f_2(a)$和函数$f_3(a)$的交点处$\max\{f(x)\}$取得最小值，为$13-4\sqrt{10}$．因此$k$的取值范围是$(-\infty,13-4\sqrt{10}]$．