每日一题[46] 三射线定理

已知二面角\(\alpha-AB-\beta\)为\(120^\circ\)，\(CD\subset\alpha\)，\(CD\perp AB\)，\(EF\subset\beta\)，\(EF\)与\(AB\)成\(30^\circ\)角，则异面直线\(CD\)与\(EF\)所成角的余弦值为________．

正确答案是\(\dfrac 14\)．

事实上，我们有一般的结论（三射线定理）．

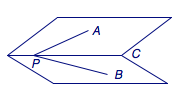
如图，\(PA\)、\(PB\)、\(PC\)分别是从\(P\)出发的三条射线，\(\angle APC\)、\(\angle BPC\)、\(\angle APB\)分别为\(\alpha\)、\(\beta\)、\(\theta\)，则二面角\(A-PC-B\)（记其大小为\(\varphi\)）满足：\[\cos\theta=\cos\alpha\cdot\cos\beta+\sin\alpha\cdot\sin\beta\cdot\cos\varphi.\]

证明如下：

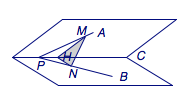
过射线\(PC\)上一点\(H\)作垂直于\(PC\)的平面，射线\(PA\)、\(PB\)分别与该平面相交于\(M\)、\(N\)两点，则\[\begin{split}\overrightarrow{PM}\cdot\overrightarrow{PN}&=\left(\overrightarrow{PH}+\overrightarrow{HM}\right)\cdot\left(\overrightarrow{PH}+\overrightarrow{HN}\right)\\&=PH^2+\overrightarrow{HM}\cdot\overrightarrow{HN}\\&=PH^2+HM\cdot HN\cdot\cos\varphi,\end{split}\]又\[\overrightarrow{PM}\cdot\overrightarrow{PN}=PM\cdot PN\cos\theta,\]于是两边同除以\(PM\cdot PN\)得\[\cos\theta=\cos\alpha\cdot\cos\beta+\sin\alpha\cdot\sin\beta\cdot\cos\varphi.\]

在今天的这道试题中，应用三射线定理，有\[\cos\theta=\cos 30^\circ\cdot\cos 90^\circ+\sin 30^\circ\cdot\sin 90^\circ\cdot\cos 120^\circ=-\frac{1}{4},\]于是所求值为\(\dfrac 14\)．