每日一题[235] 弧长与折线长

2013年高考江西卷理科数学第10题（选择压轴题，有不影响本质的改动）：

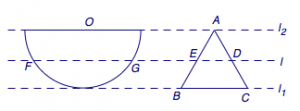
如图，半径为$1$的半圆$O$与等边三角形$ABC$夹在平行线$l_1$、$l_2$之间，$l\parallel l_1$，$l$与半圆相交于$F$、$G$两点，与三角形$ABC$两边相交于$E$、$D$两点．设弧$FG$的长为$x$（$0<x<\pi$），$y=EB+BC+CD$，若$l$从$l_1$平行移动到$l_2$，则函数$y=f(x)$的图象大致是_______．

                                                 

---

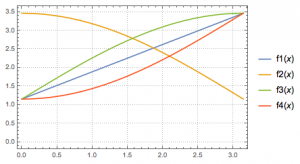
正确的答案是 $f_4(x)$．

解    分别计算特殊位置：

（1）$x=0$时，$y=BC$；

（2）$x=\pi$时，$y=AB+BC+CA=3BC$；

（3）$x=\dfrac {2\pi}3$时，$y=2BC$；

按线性递增计算，若函数图象满足（1）（2），那么函数图象在$x=\dfrac{2\pi}3$处的取值为

$$\dfrac{3BC-BC}{\pi-0}\cdot\dfrac{2\pi}3+BC=\dfrac 73BC,$$ 由此可知函数图像应在连接点$\left(0,\dfrac{2\sqrt 3 }3\right)$和点$\left(\dfrac{2\pi}3，\dfrac{14\sqrt 3}9\right)$的线段下方，只有 $f_4(x)$ 符合题意．

事实上，有

$$y=-\dfrac{4\sqrt 3}3\cos\dfrac{x}{2}+2\sqrt 3,0<x<\pi.$$

---

注    如图，将条件”等边三角形“中的边$AB$和$AC$加以改写会使得题目的图形更加直接了当．