如图,将正方形\(ABCD\)翻折,使点\(B\)落在\(CD\)边上点\(E\)处(不与\(C,D\)重合),压平后得到折痕\(MN\).设\(\dfrac {CE}{CD}=\dfrac 1n\),则\(\dfrac {AM}{BN}=\) (用含\(n\)的式子表示). 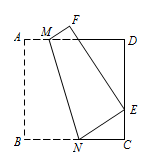 答案 \(\dfrac {(n-1)^2}{n^2+1}\).
答案 \(\dfrac {(n-1)^2}{n^2+1}\).
解 方法一 这个方法比较常规,利用翻折的性质,得到\(BM=ME\).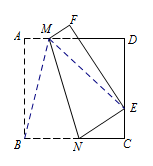 由已知,不妨设\(BC=n,CE=1\),
由已知,不妨设\(BC=n,CE=1\),
在\(\mathrm {Rt}\triangle NEC\)中,根据勾股定理得\[EN^2=CN^2+CE^2,\] 解得\[BN=\dfrac {n^2+1}{2n}.\] 又因为\[AB^2+AM^2=MD^2+DE^2,\]解得\[AM=\dfrac {(n-1)^2}{2n}.\]故 \[\dfrac {AM}{BN}=\dfrac {(n-1)^2}{n^2+1}.\]
方法二 建立平面直角坐标系,通过求直线\(MN\)的解析式,得到\(AM,BN\)的长,使问题得到解决.
如图,以\(B\)为坐标原点建立平面直角坐标系,易得\(A(0,n),B(0,0),C(n,0),D(n,n),E(n,1)\).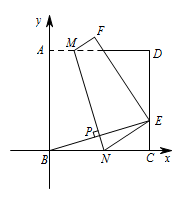 求得直线\(BE\)解析式为\[y=\dfrac xn.\] 因为\(MN\)垂直平分\(BE\),则\(P(\dfrac n2,\dfrac 12)\),从而得直线\(MN\)的解析式为\[y=-nx+\dfrac {n^2+1}2.\] 将\(y=0\),\(y=n\)代入即可得\(AM,BN\),从而\[\dfrac {AM}{BN}=\dfrac {(n-1)^2}{n^2+1}.\]
求得直线\(BE\)解析式为\[y=\dfrac xn.\] 因为\(MN\)垂直平分\(BE\),则\(P(\dfrac n2,\dfrac 12)\),从而得直线\(MN\)的解析式为\[y=-nx+\dfrac {n^2+1}2.\] 将\(y=0\),\(y=n\)代入即可得\(AM,BN\),从而\[\dfrac {AM}{BN}=\dfrac {(n-1)^2}{n^2+1}.\]
翻折问题我们常用的方法是寻找翻折前后的不变量,今天引入一个新的媒介——平面直角坐标系,通过直线方程来解决翻折问题.当正方形、矩形、等腰三角形等图形中涉及数量关系比较多的时候,我们不妨试一下这种方法,思路清晰易懂.
利用直角坐标系解决翻折问
《利用直角坐标系解决翻折问》有一条回应
发表回复
要发表评论,您必须先登录。

Pingback引用通告: [平面几何]利用直角坐标系解决翻折问题(二) | 数海拾贝内容系统