2011年高考数学北京卷第14题 (填空压轴题):
曲线$C$是平面内与两个定点$F_1(-1,0)$和$F_2(1,0)$的距离之积等于常数$a^2(a>1)$的点的轨迹.给出下列三个结论:
①曲线$C$过坐标原点;
②曲线$C$关于坐标原点对称;
③若点$P$在曲线$C$上,则$\triangle F_1PF_2$的面积不大于$\dfrac{1}{2}a^2$.
其中所有正确结论的序号是_____.
正确答案是②③.
解 我们很熟悉的问题是:“曲线$C$是平面内与两个定点$F_1(-1,0)$和$F_2(1,0)$的距离之比等于常数$\lambda$($\lambda>1$)的点的轨迹,$\cdots$”(见阿波罗尼斯圆).研究这个问题所用的方法为用直译法写出轨迹方程,然后通过研究代数方程来探索轨迹的几何性质.
理解题意后可以写出轨迹方程\[\sqrt{(x+1)^2+y^2}\cdot\sqrt{(x-1)^2+y^2}=a^2.\]据此考查三个结论:
①曲线$C$过坐标原点,即原点坐标$(0,0)$是方程的解,显然不正确;
②曲线$C$关于坐标原点对称,即若$(x,y)\in C$,则$(-x,-y)\in C$,显然正确;
③选用合适的面积公式\[\begin{split}S_{\triangle F_1PF_2}&=\dfrac 12\cdot|PF_1|\cdot |PF_2|\cdot \sin\angle F_1PF_2\\&\leqslant \dfrac 12a^2.\end{split}\]因此③正确.
注 结论③可以引发我们进一步探索曲线$C$的有界性.
1.根据结论③,曲线$C$被限制在直线$y=\dfrac 12a^2$和$y=-\dfrac 12a^2$之间;
2.在$x$轴上可以找到两点$A(t,0)(t>0)$和$B(-t,0)$使得$(t-1)(t+1)=a^2$,即$$t=\sqrt{a^2+1}.$$容易证明曲线$C$被限制在直线$x=t$和$x=-t$之间.
在此基础上结合结论②进一步思考曲线$C$的封闭性.
因为曲线$C$关于$x$和$y$轴对称,因此我们只需要考虑曲线$C$在第一象限的情况.
因为$a>1$,所以在$y$轴上可以找到两点$E(0,s)$和$F(0,-s)$满足$$\sqrt{1^2+s^2}\cdot\sqrt{1^2+s^2}=a^2,$$其中$s>0$.
考虑曲线在第一象限内的情况,当$x$的值给定时,$$\sqrt{(x+1)^2+y^2}\cdot\sqrt{(x-1)^2+y^2}$$关于$y$单调递增且最小值为$$\sqrt{(x+1)^2+0^2}\cdot\sqrt{(x-1)^2+0^2}=|1-x^2|<a^2,$$因此每个$x$有且只有一个$y$与之对应,曲线$C$在第一象限内可以看作是连接$A$和$E$的函数图象.
综上,就证明了曲线$C$是一条封闭曲线.
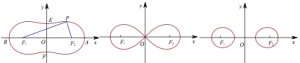
事实上,当$a>1$、$a=1$、$a<1$时,曲线$C$如下图左、中、右所示:
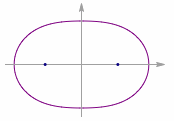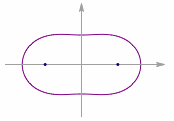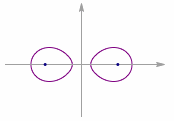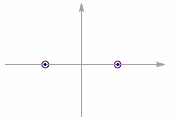
平面上到两个定点(距离为$2c$)的距离之积为定值($a^2$)的点的轨迹称为卡西尼卵形线,这两个定点叫作焦点,随着$a$与$c$的大小关系变化卵形线的形状会发生变化,如下图: