每日一题[202] 又见三射线

2014年全国高中数学联赛山东省预赛第5题：

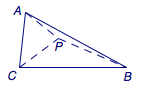
已知直角三角形$ABC$的两条直角边$AC=2$，$BC=3$，$P$为斜边$AB$上一点，将$CP$将此三角形折成直二面角$A-CP-B$，当$AB=\sqrt 7$时，二面角$P-AC-B$的值为_______．

---

正确答案是$\arctan \sqrt 2$．

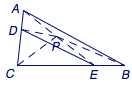
如图，在平面$PCB$内过$P$作直二面角$A-CP-B$的棱$CP$的垂线交边$BC$于$E$，则$EP\perp ACP$．

于是在平面$PAC$中过$P$作二面角$P-AC-B$的棱$AC$的垂线，垂足为$D$，连接$DE$，则$\angle PDE$为二面角$P-AC-B$的平面角，且$\tan\angle PDE=\dfrac{EP}{PD}$．

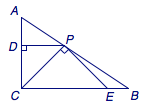
根据每日一题[46] 三射线定理，有

$$\cos\angle ACB=\cos\angle ACP\cdot\cos\angle BCP,$$ 于是 $$\dfrac{AC^2+BC^2-AB^2}{2\cdot AC\cdot BC}=\cos\angle ACP\cdot\sin \angle ACP,$$ 解得 $$\angle ACP=\dfrac {\pi}{4},$$ 如图．

因此所求二面角$P-AC-B$的值为$\arctan \sqrt 2$．