每日一题[200] 四次方程的韦达定理

2014年全国高中数学联赛吉林省预赛第10题：

方程组

$$\begin{cases}a+b+c+d=-2,\\ab+ac+ad+bc+bd+cd=-3,\\bcd+acd+abd+abc=4,\\abcd=3,\end{cases}$$ 的一组实数解$(a,b,c,d)$为_______．

---

正确答案是$\left(\dfrac{-\sqrt{13}-1}2,\dfrac{\sqrt{13}-1}2,\dfrac{-\sqrt 5-1}2,\dfrac{\sqrt 5-1}2\right)$．

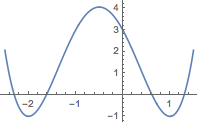
设$f(x)=(x-a)(x-b)(x-c)(x-d)$，则根据已知条件可得

$$f(x)=x^4+2x^3-3x^2-4x+3,$$ 因此$a,b,c,d$分别是方程 $$x^4+2x^3-3x^2-4x+3=0$$ 的四个实数根．

为了消去$x^3$项，作换元$t=x+\dfrac 12$，整理得

$$16t^4-72t^2+65=0,$$ 解得 $$t^2=\dfrac 54\lor t^2=\dfrac {13}{4},$$ 进而即得原方程组的一组实数解为$\left(\dfrac{-\sqrt{13}-1}2,\dfrac{\sqrt{13}-1}2,\dfrac{-\sqrt 5-1}2,\dfrac{\sqrt 5-1}2\right)$．

---

注    可以参考  每日一题[29] 一般三次方程的解法．