每日一题[170] 化椭为圆

2015年高考山东卷理科数学第20题（解析几何大题）：

平面直角坐标系$xOy$中，已知椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$的离心率为$\dfrac{\sqrt 3}2$，左、右焦点分别是$F_1$、$F_2$．以$F_1$为圆心，以$3$为半径的圆与以$F_2$为圆心，以$1$为半径的圆相交，且交点在椭圆$C$上．

（1）求椭圆$C$的方程；

（2）设椭圆$E:\dfrac{x^2}{4a^2}+\dfrac{y^2}{4b^2}=1$，$P$为椭圆$C$上任意一点，过点$P$的直线$y=kx+m$交椭圆$E$于$A$、$B$两点，射线$PO$交椭圆$E$于点$Q$．① 求$\dfrac{|OQ|}{|OP|}$的值；② 求$\triangle ABQ$面积的最大值．

（1）解    显然椭圆$C$的长轴长为$4$，于是方程为$\dfrac{x^2}4+y^2=1$．

（2）解    ① $2$；

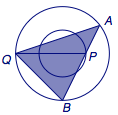
② 如图，将椭圆$C$和椭圆$E$伸缩变换为圆$C':x^2+y^2=4$和圆$E':x^2+y^2=16$．设变换后$AB$与$PQ$所成角为$\theta$，原点$O$到直线$AB$距离为$d$，则 $$\begin{split}S_{\triangle QAB}&=\dfrac 12\sin\theta \cdot AB\cdot PQ\\&=\dfrac 12 \cdot \dfrac{d}2\cdot 2\sqrt{4^2-d^2}\cdot 6\\&=3\sqrt{d^2\left(16-d^2\right)},\end{split}$$ 由于$0\leqslant d^2\leqslant 4$，于是当$d^2=4$时，三角形$QAB$的面积取得最大值为$12\sqrt 3$．于是变换前三角形$QAB$面积的最大值为$6\sqrt 3$．