2015年高考数学湖北卷理科数学第14题(填空压轴题):
如图,圆\(C\)与\(x\)轴相切于点\(T(1,0)\),与\(y\)轴正半轴交于两点\(A\)、\(B\)(\(B\)在\(A\)的上方),且\(AB=2\).
(1)圆\(C\)的标准方程为_______;
(2)过点\(A\)任作一条直线与圆\(O:x^2+y^2=1\)相交于\(M\)、\(N\)两点,下列三个结论:
① \(\dfrac{NA}{NB}=\dfrac{MA}{MB}\);
② \(\dfrac{NB}{NA}-\dfrac{MA}{MB}=2\);
③ \(\dfrac{NB}{NA}+\dfrac{MA}{MB}=2\sqrt 2\).
其中正确结论的序号是_______.(写出所有正确结论的序号)
 正确答案是(1)\((x-1)^2+\left(y-\sqrt 2\right)^2=1\);(2)①②③.
正确答案是(1)\((x-1)^2+\left(y-\sqrt 2\right)^2=1\);(2)①②③.
(1)由于圆\(C\)与\(x\)轴相切于\((1,0)\),于是弦\(AB\)与圆心的距离为\(1\),进而可得圆的半径为\(\sqrt 2\),于是圆\(C\)的方程为\[(x-1)^2+\left(y-\sqrt 2\right)^2=2.\]
(2)点\(A\left(0,\sqrt 2-1\right)\),点\(B\left(0,\sqrt 2+1\right)\),设圆\(O\)与\(y\)轴的交点分别为\(P\)、\(Q\),如图.
由于\[\overrightarrow{AP}=\left(\sqrt 2-1\right)\overrightarrow{PB},\\\overrightarrow{AQ}=-\left(\sqrt 2-1\right)\overrightarrow{QB},\]于是以\(PQ\)为直径的圆\(O\)上的点到\(A\)与到\(B\)的距离之比\[\dfrac{MA}{MB}=\dfrac{NA}{NB}=\sqrt 2-1,\]因此命题①②③均正确.
注 这里用到了阿波罗尼斯圆,也可以参考每日一题[39] 阿波罗尼斯圆.


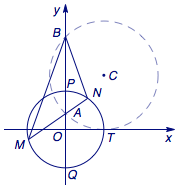
我的过程:由\(AM\cdot AN=AP\cdot AQ=OA\cdot AB\)得到,\(O,B,M,N\)四点共圆,连结\(OM,ON\),有\(\angle{ONA}=\angle{OBN}\),所以\(\triangle OAN\backsim\triangle ONB\),所以\(\dfrac{NA}{NB}=\dfrac{OA}{ON}=\sqrt{2}-1\),从而得到相应结果。
图怎么贴。。。
现在可以贴图了:)