每日一题[39] 阿波罗尼斯圆

已知三角形$ABC$中，$AB:AC=\sqrt 2:1$，$BC=2$，求三角形$ABC$面积的最大值．

 法一    利用阿波罗尼斯圆  如图，三角形$ABC$的顶点$A$的轨迹为以$MN$为直径的圆（想想看，为什么？），其中 $$\overrightarrow{BM}=\sqrt 2\overrightarrow{MC},\overrightarrow{BN}=-\sqrt 2\overrightarrow{NC}.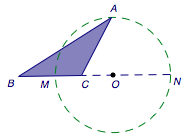$$ 不难求得 $$CM=2\left(\sqrt 2-1\right),CN=2\left(\sqrt 2+1\right).$$ 于是$BC$边上的高的最大值为圆的半径 $$\dfrac {MN}2=\dfrac{CM+CN}2=2\sqrt 2.$$ 进而三角形$ABC$面积的最大值为 $$\dfrac 12BC\cdot 2\sqrt 2=2\sqrt 2.$$

法二    利用海伦公式 令$AB=2\sqrt 2t$，$AC=2t$，则三角形$ABC$的半周长 $$p=\left(\sqrt 2+1\right)t+1.$$ 由海伦公式 $$S_{\triangle ABC}=\sqrt{p\cdot (p-AB)\cdot (p-BC)\cdot (P-CA)},$$ 将$AB$，$BC$，$CA$的长度代入，并整理得 $$\begin{split}S_{\triangle ABC}&=\sqrt{\left[t^2-\left(\sqrt 2-1\right)^2\right]\cdot\left[\left(\sqrt 2+1\right)^2-t^2\right]}\\&\leqslant\dfrac{\left[t^2-\left(\sqrt 2-1\right)^2\right]+\left[\left(\sqrt 2+1\right)^2-t^2\right]}2\\&=2\sqrt 2.\end{split}$$ 等号当且仅当$t^2=3$时取得．

注    事实上，平面上到两顶点的距离的平方和为定值的点的轨迹也是圆．