每日一题[157]端点定乾坤

2015年高考福建卷理科数学第20题（压轴题）：

已知函数$f(x)=\ln (1+x)$，$g(x)=kx$，$k\in \mathcal R$．

（1）证明：当$x>0$时，$f(x)<x$；

（2）证明：当$k<1$时，存在$x_0>0$，使得对任意$x\in (0,x_0)$，恒有$f(x)>g(x)$；

（3）确定$k$的所有可能取值，使得存在$t>0$，对任意$x\in (0,t)$，恒有$\left|f(x)-g(x)\right|<x^2$．

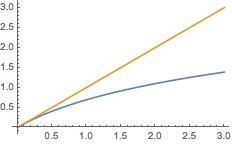
（1）证明    根据题意，当$x>0$时，有 $$\left(f(x)-x\right)'=\dfrac 1{1+x}-1=\dfrac{-x}{1+x}<0,$$ 于是命题得证（如图）．

（2）证明    考虑 $$\left(f(x)-g(x)\right)'=\dfrac{1}{x+1}-k,$$ 于是当$0<x<\dfrac 1k-1$时必然有 $$\left(f(x)-g(x)\right)'>0,$$ 于是函数$f(x)-g(x)$在$\left(0,\dfrac 1k-1\right)$上单调递增，又$f(0)-g(0)=0$，于是取$x_0=\dfrac 1k-1$即可证明命题成立．

（3）解    根据题意当$x\to 0+$时，有 $$-x^2<f(x)-g(x)<x^2,$$ 即 $$\begin{cases}\ln (1+x)-kx-x^2<0,\\\ln(1+x)-kx+x^2>0,\end{cases}$$ 记 $$\begin{split}h_1(x)=\ln (1+x)-kx-x^2,\\h_2(x)=\ln (1+x)-kx+x^2,\end{split}$$ 此时注意到 $$h_1(0)=h_2(0)=0,$$ 于是 $$h_1'(0)\leqslant 0 \leqslant h_2'(0),$$ 即 $$1-k\leqslant 0 \leqslant 1-k,$$ 因此$k=1$．

事实上当$k=1$时，在$0<x<1$时，有 $$\begin{split}h_1'(x)=\dfrac{1}{1+x}-1-2x=\dfrac{-2x^2-3x}{1+x}<0,\\h_2'(x)=\dfrac{1}{1+x}-1+2x=\dfrac{x+2x^2}{1+x}>0,\end{split}$$ 结合 $$h_1(0)=h_2(0)=0,$$ 于是有 $$h_1(x)<0<h_2(x)$$ 成立，即 $$\left|f(x)-g(x)\right|<x^2$$ 成立，符合题意．