每日一题[991]左右不逢源

在$1,2,3,4,5,6,7,8,9,10,11,12,13$共$13$个数中挑出$k$个数，使得这$k$个数中任意两个的差都不是$5$和$8$，则$k$的最大值是_______．

---

正确答案是$6$．

分析与解　如图．将$13$个数排成一圈，其中任何相邻的数都不能同时取．从$1$开始逆时针顺序把数染成实心和空心，则所有空心圈对应的数符合题意，共$6$个．且若$k$超过$6$个，则必然会出现两个数相邻，因此$k$的最大值为$6$．

---

下面给出一道练习：

在不超过 $99$ 的正整数中选出 $50$ 个不同的正整数，已知这 $50$ 个数中任两个的和都不等于 $99$，也不等于 $100$．这 $50$ 个数的和可能等于_______．

解　$3725$；

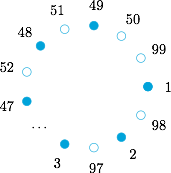
可以将这$99$个数排成一圈，从$1$开始，将$1$染成实心点，与$1$的和为$99$或$100$的点染成空心点，与空心点和为$99$或$100$的点染成实心点，如下图：

满足条件的$50$个数只可能为所有标为空心点的数，即$50,51,52,\cdots,98,99$，所以它们的和为

$$50+51+\cdots+98+99=3725.$$