注意:所有题目均为单项选择题,共$20$小题.
1.已知函数$f(x)$是连续的偶函数,且当$x>0$时$f(x)$是严格单调函数,则满足$f(x)=f \left(\dfrac{x+3}{x+4}\right)$的所有$x$之和是( )
A.$-1$
B.$-3$
C.$-5$
D.$-8$
2.设集合$A=\left\{x\left|\ x=\dfrac{1}{2}k+\dfrac{1}{4},k\in\mathbb{Z}\right.\right\}$,$B=\left\{x\left|\ x=\dfrac{1}{4}k+\dfrac{1}{2},k\in\mathbb{Z}\right.\right\}$,则$A$与$B$的关系是( )
A.$A$是$B$ 在有理数集中的补集
B.$A$是$B$的真子集
C.$B$是$A$的真子集
D.以上均不对
3.方程$x^2-(3a+2)x+2a-1=0$的两个实根中一个大于$3$,另一个小于$3$,则$a$的取值范围是( )
A.$a>\dfrac{2}{7}$
B.$a>\dfrac{2}{9}$
C.$a<\dfrac{2}{7}$
D.$a<\dfrac{2}{9}$
4.设实数$a,b,c$均不为$0$,且满足$\dfrac{b+c}{a}=\dfrac{c+a}{b}=\dfrac{a+b}{c}$,则$\dfrac{abc}{(a+b)(b+c)(c+a)}$的值是( )
A.$\dfrac{1}{8}$
B.$1$
C.$-1$
D.以上均不对
5.设$\dfrac{3\pi}{2}<\alpha<2\pi$,则$\sqrt{\dfrac{1}{2}+\dfrac{1}{2}\sqrt{\dfrac{1}{2}+\dfrac{1}{2}\cos{2\alpha}}}=$( )
A.$\cos{\dfrac{\alpha}{2}}$
B.$\sin{\dfrac{\alpha}{2}}$
C.$-\cos{\dfrac{\alpha}{2}}$
D.$-\sin{\dfrac{\alpha}{2}}$
6.设一个圆锥的底面积为$10$,它的侧面展开成平面图后为一个半圆,则此圆锥的侧面积是( )
A.$10$
B.$20$
C.$30$
D.$40$
7.设$a \geqslant 1$,且对任意$x\in[1,2]$,不等式$x|x-a|+\dfrac{3}{2}\geqslant a$恒成立,则实数$a$的取值范围是( )
A.$\left[1,\dfrac{3}{2}\right]\cup\left[\dfrac{5}{2},+\infty\right)$
B.$\left[1,\dfrac{5}{4}\right]\cup\left[\dfrac{5}{2},+\infty\right)$
C.$\left[\dfrac{5}{4},\dfrac{3}{2}\right]\cup\left[\dfrac{5}{2},+\infty\right)$
D.以上均不对
8.设$m>0$,$p:\left|1-\dfrac{x-1}{3}\right|\leqslant 2$,$q:x^2-2x+1-m^2\leqslant 0$,若$\neg p$是$\neg q$的必要而不充分条件,则$m$的取值范围是( )
A.$[1,+\infty)$
B.$[3,+\infty)$
C.$[6,+\infty)$
D.$[9,+\infty)$
9.设$\dfrac{\pi}{4}<\theta<\dfrac{\pi}{2}$,把复数$z_1=2\sin{\theta}+\mathrm{i}\cos{\theta}$在复平面上对应的向量按顺时针旋转$\dfrac{3\pi}{4}$后得到的复数为$z_2=r \left(\cos{\varphi}+\mathrm{i}\sin{\varphi}\right)$,那么$\tan{\varphi}=$( )
A.$\dfrac{2\tan{\theta}+1}{2\tan{\theta}-1}$
B.$\dfrac{2\tan{\theta}-1}{2\tan{\theta}+1}$
C.$\dfrac{1}{2\tan{\theta}+1}$
D.$\dfrac{1}{2\tan{\theta}-1}$
10.函数$f(x)=\dfrac{x^2-x-1}{x^2+x+1}$的最大值与最小值的和是( )
A.$\dfrac{5}{3}$
B.$\dfrac{2}{3}$
C.$1$
D.$-\dfrac{2}{3}$
11.设$m,n$为任意正整数,函数$f(m,n)$的取值也是正整数,且满足$f(1,1)=1$,$f(m,n+1)=f(m,n)+2$,$f(m+1,1)=2f(m,1)$,则$f(2016,2015)=$( )
A.$2^{2015}+2015$
B.$2^{2016}+2016$
C.$2^{2015}+4028$
D.$2^{2016}+4028$
12.设有命题$A,B,C,D,E$,其中$A$是$B$的充分条件,$B$是$C$的充要条件,$\neg A$是$E$的充分条件,$D$是$C$的必要条件,则$D$是$\neg E$的( )
A.充分条件
B.必要条件
C.充要条件
D.既不充分也不必要条件
13.设直角梯形的高为$2$,其两条对角线交点为$P$,以它的两底中点的连线为直径的圆与此梯形的直腰相交于点$E$和$F$,则$P$到$E$和$F$这两点的距离之和为( )
A.$\sqrt{2}$
B.$2$
C.$1$
D.以上均不对
14.一种正十二面体的骰子,$12$个表面分别写有$1$到$12$的$12$个数字,则扔一对这样的骰子,可能出现的结果种数是( )
A.$144$
B.$132$
C.$72$
D.$78$
15.设实数$x_1 \geqslant x_2 \geqslant \cdots \geqslant x_{2016}>1$,且$x_1+x_2+\cdots+x_{2016}=2018$,则$\ln{\left(x_1\right)}\ln{\left(x_{2016}\right)}$与$\dfrac{1}{2015}$的大小关系是( )
A.$\ln{\left(x_1\right)}\ln{\left(x_{2016}\right)}>\dfrac{1}{2015}$
B.$\ln{\left(x_1\right)}\ln{\left(x_{2016}\right)}=\dfrac{1}{2015}$
C.$\ln{\left(x_1\right)}\ln{\left(x_{2016}\right)}<\dfrac{1}{2015}$
D.以上都有可能
16.设角$\alpha=\dfrac{\pi}{7}$,则$\sin^2\alpha+\sin^2{2\alpha}+\sin^2{3\alpha}$的值为( )
A.$\dfrac 74$
B.$1$
C.$\dfrac 78$
D.以上均不对
17.已知$x>0$时,不等式$[(a-1)x-1](x^2-ax-1)\geqslant 0$恒成立,则实数$a$的取值范围是( )
A.$0\leqslant a\leqslant \dfrac 32$
B.$1\leqslant a\leqslant \dfrac 32$
C.$a=\dfrac 32$
D.不存在这样的$a$
18.已知$\alpha ,\beta\in\left(0,\dfrac{\pi}{2}\right)$,且$\sin\beta=2\cos(\alpha+\beta)\sin\alpha$,则$\tan\beta$具有( )
A.最大值$\sqrt 3$
B.最小值$\sqrt 3$
C.取不到最大或最小值
D.以上均不对
19.设实数$a,b,c$满足$a,b,c\geqslant 1$且$ab\sqrt{c-1}+ac\sqrt{b-1}+bc\sqrt{a-1}=\dfrac 32abc$,则$a,b,c$之间的大小关系是( )
A.$a>b>c$
B.$a=b=c$
C.$a<b<c$
D.不能比较大小
20.设三角形$ABC$的中线$AL$与$BM$相交于点$K$,若$K,L,C,M$四点共圆,则$\dfrac{AB}{KC}$的值是( )
A.$1$
B.$2$
C.$\sqrt 3$
D.不能确定
参考答案与解析
1.D.
根据题意,有$x=\dfrac{x+3}{x+4}$或$x=-\dfrac{x+3}{x+4}$,即$x^2+3x-3=0$,或$ x^2+5x+3=0$,于是题中方程的所有解之和为$(-3)+(-5)=-8$.
2.B.
注 此题来源于2002年全国卷的第5题:
设集合$M=\left\{x\left|\ x=\dfrac{1}{2}k+\dfrac{1}{4},k\in\mathbb{Z}\right.\right\}$,$N=\left\{x\left|\ x=\dfrac{1}{4}k+\dfrac{1}{2},k\in\mathbb{Z}\right.\right\}$,则( )
A.$M=N$
B.$M\subsetneqq N$
C.$M\supsetneqq N$
D.$M\cap N=\varnothing$
3.A.
设$f(x)=x^2-(3a+2)x+2a-1$,则问题等价于$f(3)<0$,解得$a>\dfrac 27$.
4.D.
设$\dfrac{b+c}{a}=\dfrac{c+a}{b}=\dfrac{a+b}{c}=k$,则$$\dfrac{abc}{(a+b)(b+c)(c+a)}=\dfrac{1}{k^3}.$$若$a-b=0$,则有$a=b=c$,于是$k=2$,所求代数式的值为$\dfrac 18$;
若$a-b\neq 0$,则根据合分比定理,有$$k=\dfrac{(b+c)-(c+a)}{a-b}=-1,$$此时$a+b+c=0$,所求代数式的值为$-1$.
5.C.
显然原式等于$\left|\cos\dfrac{\alpha}2\right|$,而$\dfrac{3\pi}4<\dfrac{\alpha}2<\pi$,于是$\cos\dfrac{\alpha}2<0$.
6.B.
设圆锥的底面半径为$r$,母线长为$l$,则有$$\begin{cases} \pi l=2\pi r,\\ \pi r^2=10,\end{cases} $$从而此圆锥的侧面积为$$\dfrac 12\pi l^2=\dfrac 12\pi \cdot 4r^2=20.$$
7.A.
令$f(x)=x|x-a|+\dfrac{3}{2}$.
情形一 若$1 \leqslant a \leqslant 2$,则\[f(x)_{\min}=f(a)=\dfrac{3}{2},\]故此时$1 \leqslant a \leqslant \dfrac{3}{2}$.
情形二 若$a>2$,则$f(x)=x(a-x)+\dfrac{3}{2}$,此时原问题等价于
$$\begin{cases}f(1)\geqslant a,\\f(2)\geqslant a,\end{cases}$$解得$a \geqslant \dfrac{5}{2}$.
综上所述,实数$a$的取值范围是$\left[1,\dfrac{3}{2}\right]\cup\left[\dfrac{5}{2},+\infty\right)$.
8.D.
由题意知$p$是$q$的充分不必要条件.$p:-2\leqslant x\leqslant 10$,设$f(x)=x^2-2x+1-m^2$,则$f(-2)\leqslant 0$,$f(10)\leqslant 0$且$f(-2)$和$f(10)$不同时为$0$,解得$m\geqslant 9$.
9.A.
由题意,设$\arg z=\alpha$,则$\tan{\alpha}=\dfrac{\cos{\theta}}{2\sin{\theta}}$,$\varphi$的终边与$\alpha-\dfrac{3\pi}{4}$的终边重合,所以
$$\tan{\varphi}=\tan{\left(\alpha-\dfrac{3\pi}{4}\right)}=\dfrac{\tan{\alpha}+1}{1-\tan{\alpha}}=\dfrac{2\tan{\theta}+1}{2\tan{\theta}-1}.$$
10.B.
方法一 根据题意,当$x=-1$时,有$f(x)=1$;当$x\ne -1$时,有$$f(x)=1-\dfrac{2}{x+1+\dfrac{1}{x+1}-1},$$于是$f(x)$的最大值为$\dfrac 53$,最小值为$-1$.
方法二 设$y=\dfrac{x^2-x-1}{x^2+x+1}$,则有$$(y-1)x^2+(y+1)x+y+1=0,$$进而$$\Delta=(y+1)^2-4(y-1)(y+1)=(y+1)(-3y+5)\geqslant 0,$$于是$y$的最大值为$\dfrac 53$,最小值为$-1$.
11.C.
由题意,$$f(2016,2015)=f(2016,1)+2\cdot 2014=f(1,1)\cdot 2^{2015}+4028=2^{2015}+4028.$$
12.B.
注意$\neg E$是$A$的充分条件,于是有$\neg E\Rightarrow A\Rightarrow B\Leftrightarrow C\Rightarrow D$.
13.B.
方法一
如图,直角梯形$ABCD$中,$AB \parallel CD$,$\angle BAD=\angle ADC=90^\circ$,$AD=2$,$AB=2a$,$CD=2b$.$M,N$分别为线段$AB,CD$的中点,对角线$AC$与$BD$交于点$P$.以$MN$为直径的圆与线段$AD$交于$E,F$两点,与线段$CD$交于$N,G$两点,连接$MG$.延长$FP$,交圆于点$K$,连接$MK$.设直线$ME$与$NF$交于点$Q$,直线$MF$与$NE$交于点$H$,作$QR\perp AD$于$R$.
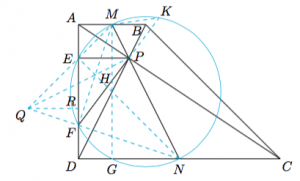 易知,$M,P,N$三点共线.因为$$\dfrac{ME}{EQ}\cdot\dfrac{QF}{FN}\cdot\dfrac{NP}{PM}=\dfrac{a}{QR}\cdot\dfrac{QR}{b}\cdot\dfrac{b}{a}=1,$$故直线$MF,NE,QP$交于一点$H$,而$H$是$\triangle QMN$的垂心,所以$$\angle EFM=\angle ENM=\angle PFH,$$因而$\stackrel\frown{ME}=\stackrel\frown{MK}$,进而有$PE=PK$.因为$$\stackrel\frown{FK}=\stackrel\frown{ME}+\stackrel\frown{MK}+\stackrel\frown{EF}=\stackrel\frown{ME}+\stackrel\frown{EF}+\stackrel\frown{FG}=\stackrel\frown{MG},$$所以$$PE+PF=PK+PF=FK=MG=AD=2.$$
易知,$M,P,N$三点共线.因为$$\dfrac{ME}{EQ}\cdot\dfrac{QF}{FN}\cdot\dfrac{NP}{PM}=\dfrac{a}{QR}\cdot\dfrac{QR}{b}\cdot\dfrac{b}{a}=1,$$故直线$MF,NE,QP$交于一点$H$,而$H$是$\triangle QMN$的垂心,所以$$\angle EFM=\angle ENM=\angle PFH,$$因而$\stackrel\frown{ME}=\stackrel\frown{MK}$,进而有$PE=PK$.因为$$\stackrel\frown{FK}=\stackrel\frown{ME}+\stackrel\frown{MK}+\stackrel\frown{EF}=\stackrel\frown{ME}+\stackrel\frown{EF}+\stackrel\frown{FG}=\stackrel\frown{MG},$$所以$$PE+PF=PK+PF=FK=MG=AD=2.$$
方法二
如图,直角梯形$ABCD$中,$AB \parallel CD$,$\angle BAD=\angle ADC=90^\circ$,$AD=2$.$M,N$分别为线段$AB,CD$的中点,对角线$AC$与$BD$交于点$P$.以$MN$为直径的圆与线段$AD$交于$E,F$两点,与线段$CD$交于$N,G$两点,连接$MG$.延长$FP$,交圆于点$K$,连接$MK$.连接$ME$与$NF$.%设直线$ME$与$NF$交于点$Q$,直线$MF$与$NE$交于点$H$,作$QR\perp AD$于$R$.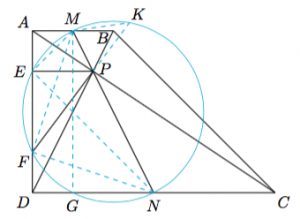 因为$$\dfrac{PM}{PN}=\dfrac{S_{\triangle PME}}{S_{\triangle PNE}}=\dfrac{EM\cdot\sin{\angle MEP}}{EN\cdot\sin{\angle NEP}},$$而$$\dfrac{PM}{PN}=\dfrac{AM}{DN}=\dfrac{EM\cdot\sin{\angle MEA}}{EN\cdot\sin{\angle NED}},$$所以$\dfrac{\sin{\angle MEP}}{\sin{\angle NEP}}=\dfrac{\sin{\angle MEA}}{\sin{\angle NED}}$.又因为$\angle MEP+\angle NEP=90^\circ$,$\angle MEA+\angle NED=90^\circ$,所以$$\angle MEP=\angle MEA,\ \angle NEP=\angle NED,$$同理,$$\angle NFP=\angle NFD,\ \angle MFP=\angle MFA,$$故$\stackrel\frown{ME}=\stackrel\frown{MK}$,进而有$ME=MK$,$PE=PK$.又因为$\stackrel\frown{KF}=\stackrel\frown{MG}$,所以$$PE+PF=PK+PF=FK=MG=AD=2.$$
因为$$\dfrac{PM}{PN}=\dfrac{S_{\triangle PME}}{S_{\triangle PNE}}=\dfrac{EM\cdot\sin{\angle MEP}}{EN\cdot\sin{\angle NEP}},$$而$$\dfrac{PM}{PN}=\dfrac{AM}{DN}=\dfrac{EM\cdot\sin{\angle MEA}}{EN\cdot\sin{\angle NED}},$$所以$\dfrac{\sin{\angle MEP}}{\sin{\angle NEP}}=\dfrac{\sin{\angle MEA}}{\sin{\angle NED}}$.又因为$\angle MEP+\angle NEP=90^\circ$,$\angle MEA+\angle NED=90^\circ$,所以$$\angle MEP=\angle MEA,\ \angle NEP=\angle NED,$$同理,$$\angle NFP=\angle NFD,\ \angle MFP=\angle MFA,$$故$\stackrel\frown{ME}=\stackrel\frown{MK}$,进而有$ME=MK$,$PE=PK$.又因为$\stackrel\frown{KF}=\stackrel\frown{MG}$,所以$$PE+PF=PK+PF=FK=MG=AD=2.$$
注 若设点$M,N$是以点$P$为焦点,直线$AD$为准线的双曲线上的两点,则此题相当于证明了双曲线的一条性质:若以双曲线的一条焦点弦$MN$为直径的圆与对应准线相交于两点$E,F$,则焦点$P$到两个交点$E,F$的距离之和等于焦点弦在准线上的投影长.抛物线也有类似的性质.
14.D.
${\rm C}_{12}^{1}+{\rm C}_{12}^{2}=78$.
15.C.
令$t_i=x_i-1>0\left(i=1,2,\cdots,2016\right)$,则
$$\ln{x_1}\ln{x_{2016}}=\ln{\left(1+t_1\right)}\ln{\left(1+t_{2016}\right)}<t_1\cdot t_{2016}\leqslant t_1\cdot\dfrac{2-t_1}{2015}\leqslant \dfrac{1}{2015}.$$
16.A.
由半角公式得$$\sin^2\alpha+\sin^2{2\alpha}+\sin^2{3\alpha}=\dfrac 32-\dfrac 12(\cos {2\alpha}+\cos{4\alpha}+\cos{6\alpha}),$$记$A=\cos {2\alpha}+\cos{4\alpha}+\cos{6\alpha}$,则有$$2\sin{2\alpha}\cdot A=\sin{4\alpha}+(\sin{6\alpha}-\sin{2\alpha})+(\sin{8\alpha}-\sin{4\alpha}).$$而$\sin{6\alpha}+\sin{8\alpha}=0$,所以$$2\sin{2\alpha}\cdot A=-\sin{2\alpha}\Rightarrow A=-\dfrac 12,$$从而得所求代数式的值为$\dfrac 74$.
17.C.
分别考虑直线$y=(a-1)x-1$与二次函数$y=x^2-ax-1$的草图,因为二次函数一定存在一个正零点与一个负零点,所以直线斜率为正,且直线与$x$轴的交点必与二次函数的正零点重合,即$\dfrac 1{a-1}$是方程$x^2-ax-1=0$的解,代入解得$a=\dfrac 32$.
也可以考虑不等式,显然有$a>1$,题中不等式可以变形为$$\left(x-\dfrac{1}{a-1}\right)(x-x_1)(x-x_2)\geqslant 0,$$其中$x_1,x_2$是方程$x^2-ax-1=0$的两根,因为$x_1x_2<0$,不妨设$x_1<x_2$,就有$x_1<0<x_2$.
而$x>0$,所以$x-x_1>0$恒成立,从而不等式$\left(x-\dfrac{1}{a-1}\right)(x-x_2)\geqslant 0$对$x>0$恒成立,因为$\dfrac 1{a-1}>0,x_2>0$,所以只能有$\dfrac 1{a-1}=x_2$,以下同上.
18.D.
因为$$\sin\beta=\sin(\alpha+\beta-\alpha)=\sin(\alpha+\beta)\cos\alpha-\cos(\alpha+\beta)\sin\alpha,$$所以由题中条件得$\tan(\alpha+\beta)=3\tan\alpha$.从而解得\[\tan\beta=\dfrac {2\tan\alpha}{3\tan^2\alpha+1}=\dfrac 2{3\tan\alpha+\frac 1{\tan\alpha}}\leqslant \dfrac{\sqrt 3}{3}.\]即$\tan\beta$有最大值$\dfrac{\sqrt 3}{3}$,当$\alpha=\beta=\dfrac{\pi}{6}$时取到.$\tan\beta$取不到最小值,当$\alpha\to\dfrac{\pi}{2}$时,$\tan\beta\to 0$.
19.B.
题中等式可以变形为$$\sqrt{\dfrac{c-1}{c^2}}+\sqrt{\dfrac{b-1}{b^2}}+\sqrt{\dfrac{a-1}{a^2}}\leqslant \dfrac 32,$$而$\sqrt{\dfrac{c-1}{c^2}}=\sqrt{\dfrac 14-\left(\dfrac 1c-\dfrac 12\right)^2}\leqslant \dfrac 12$,所以只能有$$\sqrt{\dfrac{c-1}{c^2}}=\sqrt{\dfrac{b-1}{b^2}}=\sqrt{\dfrac{a-1}{a^2}}=\dfrac 12,$$解得$a=b=c=2$.
也可以换元,令$$x=\sqrt{a-1},y=\sqrt{b-1},z=\sqrt{c-1},$$则有$x,y,z\geqslant 0$且题中条件变为\[\begin{split} \sum_{cyc}{2z(x^2+1)(y^2+1)}=&3(x^2+1)(y^2+1)(z^2+1)\\\leqslant&\sum_{cyc}(z^2+1)(x^2+1)(y^2+1)\\=&3(x^2+1)(y^2+1)(z^2+1).\end{split}\]所以等号必须成立,有$x=y=z=1$,从而$a=b=c=2$.
20.C.
连结$CK$并延长,使它交$AB$边于点$D$,连结$LM$,交$CD$于点$E$,如图: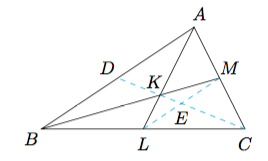 由题意知$K$是$\triangle ABC$的重心,所以$D$为$AB$的中点,$E$为$CD$的中点,也为$LM$的中点,且$K$为$CD$的靠近$D$的三等分点.记$KE=m$,则$CD=6m,CE=3m$.
由题意知$K$是$\triangle ABC$的重心,所以$D$为$AB$的中点,$E$为$CD$的中点,也为$LM$的中点,且$K$为$CD$的靠近$D$的三等分点.记$KE=m$,则$CD=6m,CE=3m$.
因为$K,L,C,M$四点共圆,由相交弦定理知$$ME\cdot LE=KE\cdot CE=3m^2,$$解得$ME=LE={\sqrt 3}m$.从而有$$\dfrac{AB}{KC}=\dfrac{2LM}{m+3m}=\dfrac{4\sqrt 3m}{4m}=\sqrt 3.$$
