据说这是2015年高三泰州二模的第14题.
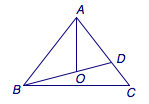
在三角形\(ABC\)中,\(D\)为边\(AC\)上一点,\(AB=AC=6\),\(AD=4\),若三角形\(ABC\)的外心\(O\)恰在线段\(BD\)上,则\(BC=\)_______.
 设\(\overrightarrow{AO}=\lambda\overrightarrow{AB}+\left(1-\lambda\right)\overrightarrow{AD}\),根据题意可知\[\overrightarrow{AO}=\lambda\overrightarrow{AB}+\dfrac{2}{3}\left(1-\lambda\right)\overrightarrow{AC},\]考虑到三角形\(ABC\)为等腰三角形,于是\[\lambda=\dfrac{2}{3}\left(1-\lambda\right),\]解得\[\lambda=\dfrac 25,\]因此有\[\overrightarrow{AO}=\dfrac 25\overrightarrow{AB}+\dfrac 25\overrightarrow{AC},\]两边对\(\overrightarrow{AB}\)作数量积,有\[\overrightarrow{AO}\cdot\overrightarrow{AB}=\dfrac 25\overrightarrow{AB}\cdot\overrightarrow{AB}+\dfrac 25\overrightarrow{AC}\cdot\overrightarrow{AB},\]由此不难解得\[\cos A=\dfrac 14,\]进而由余弦定理得\[BC^2=AB^2+AC^2-2AB\cdot AC\cos A=54,\]于是\[BC=3\sqrt 6.\]
设\(\overrightarrow{AO}=\lambda\overrightarrow{AB}+\left(1-\lambda\right)\overrightarrow{AD}\),根据题意可知\[\overrightarrow{AO}=\lambda\overrightarrow{AB}+\dfrac{2}{3}\left(1-\lambda\right)\overrightarrow{AC},\]考虑到三角形\(ABC\)为等腰三角形,于是\[\lambda=\dfrac{2}{3}\left(1-\lambda\right),\]解得\[\lambda=\dfrac 25,\]因此有\[\overrightarrow{AO}=\dfrac 25\overrightarrow{AB}+\dfrac 25\overrightarrow{AC},\]两边对\(\overrightarrow{AB}\)作数量积,有\[\overrightarrow{AO}\cdot\overrightarrow{AB}=\dfrac 25\overrightarrow{AB}\cdot\overrightarrow{AB}+\dfrac 25\overrightarrow{AC}\cdot\overrightarrow{AB},\]由此不难解得\[\cos A=\dfrac 14,\]进而由余弦定理得\[BC^2=AB^2+AC^2-2AB\cdot AC\cos A=54,\]于是\[BC=3\sqrt 6.\]

为什么cosA=¼?
好吧,我知道了将AO转化为AB的一半