每日一题[531]谁主沉浮

我们知道，当$x\in \left(0,\dfrac{\pi}{2} \right)$时，$0<\sin x<x$而$\tan x>x>0$，那么$\sin x\cdot \tan x$和$x^2$的大小关系究竟如何呢？

“每日一题[428] 谁是赢家”这篇文章给出了上述问题的解答．

类似的，我们知道，当$x>0$时，$\mathrm{e} ^x-1>x>0$而$0<\ln (1+x)<x$，那么$\left( \mathrm{e}^x-1\right)\cdot \ln (1+x)$与$x^2$之间的大小关系如何呢？$\mathrm{e} ^x-1$与$\ln (1+x)$究竟谁主沉浮？请看下题：

已知$x>0$，求证：$\left( \mathrm{e}^x-1\right)\cdot \ln (1+x)>x^2$．

---

方法一    令$f(x)=\dfrac{\ln (1+x)}{x}$，$x\in (0,+\infty)$，因为

$$f'(x)=\dfrac{\dfrac{x}{x+1}-\ln (1+x) }{x^2}<0,$$ 所以$f(x)$在$(0,+\infty)$上单调递减．

注意到同底数的指对函数之间互为反函数的关系，我们有

$$f\left(\mathrm{e} ^x-1\right)=\dfrac{x}{\mathrm{e} ^x-1}.$$

再注意到，当$x>0$时，$\mathrm{e} ^x-1>x>\ln (1+x)>0$，故有

$$f(x)>f\left(\mathrm{e} ^x-1\right),$$ 即 $$\dfrac{\ln (1+x)}{x}>\dfrac{x}{\mathrm{e} ^x-1},$$ 变形即得$\left( \mathrm{e}^x-1\right)\cdot \ln (1+x)>x^2$．

方法二    易证，当$x>0$时，

$$\mathrm{e} ^x-1>x+\dfrac{x^2}{2}>0,\ \ln(1+x)>\dfrac{2x }{x+2}>0,$$ 所以 $$\begin{split}\left( \mathrm{e}^x-1\right)\cdot \ln (1+x)&>\left(x+\dfrac{x^2}{2} \right)\cdot \dfrac{2x}{x+2}\\&=\dfrac{x\left(x^2+2x\right) }{x+2}\\&=x^2. \end{split}$$

注    因为$x\in (-\infty,+\infty)$时，有

$$\mathrm{e} ^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots,$$ 所以当$x>0$时，有 $$\mathrm{e} ^x-1>x+\dfrac{x^2}{2}>0.$$

因为$x\in (-1,1)$时，有

$$\ln (1+x)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4}+\cdots$$ 与 $$\ln (1-x)=-x-\dfrac{x^2}{2}-\dfrac{x^3}{3}-\dfrac{x^4}{4}-\cdots$$ 同时成立，故$x\in (-1,1)$时，有 $$\ln \dfrac{1+x}{1-x}=2\left(x+\dfrac{x^3}{3}+\dfrac{x^5}{5}+\cdots  \right) ,$$ 所以若$x\in (0,1)$，则 $$\ln \dfrac{1+x}{1-x}>2x.$$

令$t=\dfrac{1+x}{1-x},\ x\in (0,1)$，则$x=\dfrac{t-1}{t+1}, \ t \in (1,+\infty)$，此时有

$$\ln t>\dfrac{2(t-1)}{t+1},$$ 所以当$x>0$时， $$\ln(1+x)>\dfrac{2x }{x+2}>0.$$

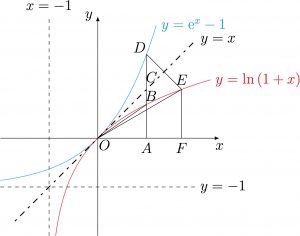
方法三    如图，

取点$A(x,0)(x>0)$，作直线$l$与$x$轴垂直，分别交函数$y=\ln{(1+x)},y=x,y=\mathrm{e} ^x-1$的图象于点$B,C,D$，设点$E$与点$D$关于直线$y=x$对称，则要证的结论等价于

$$\left|AD\right|\cdot\left|AB\right|>\left|AC\right|^2.$$ 由于函数$y=\ln{(1+x)}$在其定义域$\left(-1,+\infty\right)$上凹，故 $$\dfrac{\left|AB\right|}{\left|AC\right|}=\dfrac{\left|AB\right|}{\left|AO\right|} =\tan{\angle AOB}>\tan{\angle EOF}=\dfrac{\left|EF\right|}{\left|OF\right|}=\dfrac{\left|AC\right|}{\left|AD\right|},$$ 所以要证的结论成立．

最后给出一道练习：当$-1\leqslant x \leqslant 1$时，证明：$\sin{x}\cdot\arcsin{x}\geqslant x^2$．