原卷$40$道题均为不定项选择题．这里收录的是回忆版试题，故将部分选择题改编为填空题．
1．已知函数$f(x)=\left(x^2+a\right)\mathrm{e}^x$有最小值，则函数$g(x)=x^2+2x+a$的零点个数为（ ）
A．$0$
B．$1$
C．$2$
D．取决于$a$的值
2．已知$\triangle ABC$的三个角$A,B,C$所对的边分别为$a,b,c$．下列条件中，能使得$\triangle ABC$的形状唯一确定的有（ ）
A．$a=1,\ b=2,\ c\in\mathbf{Z}$
B．$A=150^\circ,\ a\sin{A}+c\sin{C}+\sqrt{2}a\sin{C}=b\sin{B}$
C．$\cos{A}\sin{B}\cos{C}+\cos{(B+C)}\cos{B}\sin{C}=0,\ C=60^\circ$
D．$a=\sqrt{3},\ b=1,\ A=60^\circ$
3．已知函数$f(x)=x^2-1$，$g(x)=\ln{x}$．下列说法中正确的有（ ）
A．$f(x)$与$g(x)$在点$(1,0)$处有公切线
B．存在$f(x)$的某条切线与$g(x)$的某条切线互相平行
C．$f(x)$与$g(x)$有且只有一个交点
D．$f(x)$与$g(x)$有且只有两个交点
4．过抛物线$y^2=4x$的焦点$F$作直线交抛物线于$A,B$两点，$M$为线段$AB$的中点．下列说法中正确的有（ ）
A．以线段$AB$为直径的圆与直线$x=-\dfrac{3}{2}$一定相离
B．$|AB|$的最小值为$4$
C．$|AB|$的最小值为$2$
D．以线段$BM$为直径的圆与$y$轴一定相切
5．已知$F_1,F_2$是椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$的左、右焦点，$P$是椭圆$C$上一点．下列说法中正确的有（ ）
A．$a=\sqrt{2}b$时，满足$\angle F_1PF_2=90^\circ$的点$P$有$2$个
B．$a>\sqrt{2}b$时，满足$\angle F_1PF_2=90^\circ$的点$P$有$4$个
C．$\triangle PF_1F_2$的周长小于$4a$
D．$\triangle PF_1F_2$的面积小于等于$\dfrac{a^2}{2}$
6．甲、乙、丙、丁四个人参加比赛，有两人获奖．比赛结果揭晓之前，四个人作了如下猜测．
甲：两名获奖者在乙、丙、丁中；
乙：我没有获奖，丙获奖了；
丙：甲、丁中有且只有一人获奖；
丁：乙说得对．
已知四个人中有且只有两个人的猜测是正确的，那么两名获奖者是（ ）
A．甲
B．乙
C．丙
D．丁
7．已知$AB$为圆$O$的一条弦（非直径），$OC\perp AB$于$C$．$P$为圆$O$上任意一点，直线$PA$与直线$OC$相交于点$M$，直线$PB$与直线$OC$相交于点$N$．以下说法正确的有（ ）
A．$O,M,B,P$四点共圆
B．$A,M,B,N$四点共圆
C．$A,O,P,N$四点共圆
D．前三个选项都不对
8．$\sin{A}+\sin{B}+\sin{C}>\cos{A}+\cos{B}+\cos{C}$是$\triangle ABC$为锐角三角形的（ ）
A．充分非必要条件
B．必要非充分条件
C．充分必要条件
D．既不充分也不必要条件
9．已知$x,y,z$为正整数，$x\leqslant y\leqslant z$，那么方程$\dfrac 1x+\dfrac 1y+\dfrac 1z=\dfrac 12$的解的组数为（ ）
A．$8$
B．$10$
C．$11$
D．$12$
10．已知集合$A=\left\{a_1,a_2,\cdots,a_n\right\}$，任取$1\leqslant i<j<k \leqslant n$，\[a_i+a_j\in A,\ a_j+a_k\in A,\ a_k+a_i\in A\]这三个式子中至少有一个成立，则$n$的最大值为（ ）
A．$6$
B．$7$
C．$8$
D．$9$
11．已知$\alpha=1^\circ$，$\beta=61^\circ$，$\gamma=121^\circ$，则下列各式中成立的有（ ）
A．$\tan{\alpha}\tan{\beta}+\tan{\beta}\tan{\gamma}+\tan{\gamma}\tan{\alpha}=3$
B．$\tan{\alpha}\tan{\beta}+\tan{\beta}\tan{\gamma}+\tan{\gamma}\tan{\alpha}=-3$
C．$\dfrac{\tan{\alpha}+\tan{\beta}+\tan{\gamma}}{\tan{\alpha}\tan{\beta}\tan{\gamma}}=3$
D．$\dfrac{\tan{\alpha}+\tan{\beta}+\tan{\gamma}}{\tan{\alpha}\tan{\beta}\tan{\gamma}}=-3$
12．已知实数$a,b,c$满足$a+b+c=1$，则$\sqrt{4a+1}+\sqrt{4b+1}+\sqrt{4c+1}$的最大值与最小值乘积属于区间（ ）
A．$(11,12)$
B．$(12,13)$
C．$(13,14)$
D．$(14,15)$
13．已知$x,y,z\in \mathbf{R}$，满足$x+y+z=1,\ x^2+y^2+z^2=1$，则下列结论正确的有（ ）
A．$xyz$的最大值为$0$
B．$xyz$的最小值为$-\dfrac{4}{27}$
C．$z$的最大值为$\dfrac{2}{3}$
D．$z$的最小值为$-\dfrac{1}{3}$
14．数列$\left\{a_n\right\}$满足$a_1=1,\ a_2=2,\ a_{n+2}=6a_{n+1}-a_{n}\left(n\in\mathbf{N}^{*}\right)$．对任意正整数$n$，以下说法中正确的有（ ）
A．$a_{n+1}^2-a_{n+2}a_{n}$为定值
B．$a_n\equiv 1\pmod 9$或$a_n\equiv 2\pmod 9$
C．$4a_na_{n+1}-7$为完全平方数
D．$8a_na_{n+1}-7$为完全平方数
15．若复数$z$满足$\left|z+\dfrac{1}{z}\right|=1$，则$|z|$可以取到的值有（ ）
A．$\dfrac{1}{2}$
B．$-\dfrac{1}{2}$
C．$\dfrac{\sqrt{5}-1}{2}$
D．$\dfrac{\sqrt{5}+1}{2}$
16．从正$2016$边形的顶点中任取若干个，顺次相连构成多边形，其中正多边形的个数为（ ）
A．$6552$
B．$4536$
C．$3528$
D．$2016$
17．已知椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$与直线$l_1:y=\dfrac 12x$，$l_2:y=-\dfrac 12x$，过椭圆上一点$P$作$l_1,l_2$的平行线，分别交$l_1,l_2$于$M,N$两点．若$|MN|$为定值，则$\sqrt{\dfrac ab}=$（ ）
A．$\sqrt{2}$
B．$\sqrt{3}$
C．$2$
D．$\sqrt{5}$
18．关于$x,y$的不定方程$x^2+615=2^y$的正整数解的组数为（ ）
A．$0$
B．$1$
C．$2$
D．$3$
19．因为实数的乘法满足交换律与结合律，所以若干个实数相乘的时候，可以有不同的次序．例如，三个实数$a,b,c$相乘的时候，可以有$(ab)c,\ (ba)c,\ c(ab),\ b(ca)\cdots$等等不同的次序．记$n$个实数相乘时不同的次序有$I_n$种，则（ ）
A．$I_2=2$
B．$I_3=12$
C．$I_4=96$
D．$I_5=120$
20．甲乙丙丁$4$个人进行网球淘汰赛，规定首先甲乙一组、丙丁一组进行比赛，两组的胜者争夺冠军．$4$个人相互比赛时的胜率如下表所示：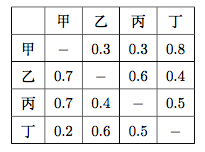
表中的每个数字表示其所在行的选手击败其所在列的选手的概率，例如甲击败乙的概率是$0.3$，乙击败丁的概率是$0.4$．那么甲赢得冠军的概率是________．
21．在正三棱锥$P-ABC$中，$\triangle ABC$的边长为$1$．设点$P$到平面$ABC$的距离为$x$，异面直线$AB$与$CP$的距离为$y$，则$\displaystyle\lim_{x\to\infty}y=$________．
22．如图，正方体$ABCD-A_1B_1C_1D_1$的棱长为$1$，中心为$O$，$\overrightarrow{BF}=\dfrac{1}{2}\overrightarrow{BC}$，$\overrightarrow{A_1E}=\dfrac{1}{4}\overrightarrow{A_1A}$，则四面体$OEBF$的体积为________．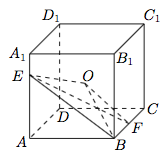
23．$\displaystyle\int_{0}^{2\pi}\left(x-\pi\right)^{2n-1}\left(1+\sin^{2n}{x}\right){\rm d} x=$________．
24．实数$x,y$满足$\left(x^2+y^2\right)^3=4x^2y^2$，则$x^2+y^2$的最大值为________．
25．$x,y,z$均为非负实数，满足$\left(x+\dfrac{1}{2}\right)^2+\left(y+1\right)^2+\left(z+\dfrac{3}{2}\right)^2=\dfrac{27}{4}$，则$x+y+z$的最大值为________，最小值为________．
26．$O$为$\triangle ABC$内一点，满足$S_{\triangle AOB}:S_{\triangle BOC}:S_{\triangle COA}=4:3:2$．设$\overrightarrow{AO}=\lambda\overrightarrow{AB}+\mu\overrightarrow{AC}$，则$\lambda+\mu=$________．
27．已知复数$z=\cos{\dfrac{2\pi}{3}}+\mathrm{i}\sin{\dfrac{2\pi}{3}}$，则$z^3+\dfrac{z^2}{z^2+z+2}=$________．
28．已知$z$为非零复数，$\dfrac{z}{10}$和$\dfrac{40}{\overline{z}}$的实部和虚部均为不小于$1$的正数，则在复平面中，$z$所对应的向量$\overrightarrow{OP}$的端点$P$运动所形成的图形面积为________．
29．若$\tan{4x}=\dfrac{\sqrt{3}}{3}$，则$\dfrac{\sin{4x}}{\cos{8x}\cos{4x}}+\dfrac{\sin{2x}}{\cos{4x}\cos{2x}}+\dfrac{\sin{x}}{\cos{2x}\cos{x}}+\dfrac{\sin{x}}{\cos{x}}=$________．
30．将$16$个数：$4$个$1$，$4$个$2$，$4$个$3$，$4$个$4$填入一个$4\times 4$的数表中，要求每行、每列都恰好有两个偶数，共有________种填法．
31．$A$是集合$\left\{1,2,3,\cdots,14\right\}$的子集，从$A$中任取$3$个元素，由小到大排列之后都不能构成等差数列，则$A$中元素个数的最大值为________．
答案及解析
1．C．
注意$f'(x)={\rm e}^x\cdot g(x)$．
2．AD．
对于选项A，由于$|a-b|<c<a+b$，于是$c$有唯一取值$2$，符合题意；
对于选项B，根据正弦定理，有$$a^2+c^2+\sqrt 2ac=b^2,$$于是可得$\cos B=-\dfrac{\sqrt 2}{2}$，$B=135^\circ$，无解；
对于选项C，条件即$$\cos A\cdot \sin (B-C)=0,$$于是$(A,B,C)=\left(90^\circ,30^\circ,60^\circ\right),\left(60^\circ,60^\circ,60^\circ\right)$，不符合题意；
对于选项D，根据正弦定理，有$\sin B=\dfrac 12$，又$A=60^\circ$，于是$B=30^\circ$，$C=90^\circ$，符合题意．
3．BD．
注意$y=x-1$为函数$g(x)$在点$(1,0)$处的切线，如图．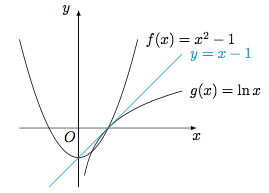
4．AB．
对于选项A，点$M$到准线$x=-1$的距离为$\dfrac 12\left(|AF|+|BF|\right)=\dfrac 12|AB|$，于是以线段$AB$为直径的圆与直线$x=-1$一定相切，进而与直线$x=-\dfrac 32$一定相离；
对于选项B和C，设$A\left(4a^2,4a\right)$，则$B\left(\dfrac{1}{4a^2},-\dfrac 1a\right)$，于是$|AB|=4a^2+\dfrac{1}{4a^2}+2$，最小值为$4$；
对于选项D，显然$BD$中点的横坐标与$\dfrac 12|BM|$不一定相等，因此命题错误．
5．ABCD．
对于选项A和B，椭圆中使得$\angle F_1PF_2$最大的点$P$位于短轴的两个端点；
对于选项C，$\triangle F_1PF_2$的周长为$2a+2c<4a$；
对于选项D，$\triangle F_1PF_2$的面积为$$\dfrac 12 \sin\angle F_1PF_2\cdot |PF_1|\cdot |PF_2|\leqslant \dfrac 12\left(\dfrac{|PF_1|+|PF_2|}2\right)^2=\dfrac 12a^2.$$
6．BD．
乙和丁同时正确或者同时错误，分类即可．
7．AC．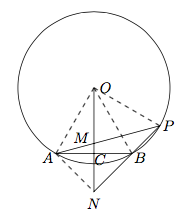
对于选项A，$\angle OBM=\angle OAM=\angle OPM$即得；
对于选项B，若命题成立，则$MN$为直径，必然有$\angle MAN$为直角，不符合题意；
对于选项C，$\angle MBN=\angle MOP=\angle MAN$即得．
8．B．
必要性：
由于$$\sin B+\sin C>\sin B+\sin\left(\dfrac{\pi}2-B\right)=\sin B+\cos B>1,$$类似的，有$\sin C+\sin A>1$，$\sin A+\sin B>1$，于是
\[\begin{split} \sin A+\sin B+\sin C&=\sin (B+C)+\sin (C+A)+\sin (A+B)\\&=\sum_{cyc}\left(\sin B+\sin C\right)\cos A\\&>\cos A+\cos B+\cos C.\end{split} \]不充分性：
当$A=\dfrac{\pi}2$，$B=C=\dfrac{\pi}4$时，不等式成立，而$\triangle ABC$并非锐角三角形．
9．B．
由于$\dfrac 12=\dfrac 1x+\dfrac 1y+\dfrac 1z\leqslant \dfrac{3}{x}$，故$3\leqslant x \leqslant 6$．
情形一 若$x=3$，则$\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{6}$，即$(y-6)(z-6)=36$，解得$$(x,y,z)=(3,7,42),\ (x,y,z)=(3,8,24),\ (x,y,z)=(3,9,18),\ (x,y,z)=(3,10,15),\ (x,y,z)=(3,12,12).$$情形二 若$x=4$，则$\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{4}$，即$(y-4)(z-4)=16$，解得$$(x,y,z)=(4,5,20),\ (x,y,z)=(4,6,12),\ (x,y,z)=(4,8,8). $$情形三 若$x=5$，则$\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{3}{10}$，此时有$$\dfrac{3}{10}=\dfrac 1y+\dfrac 1z\leqslant \dfrac 2y,$$于是$y\leqslant \dfrac{20}3$，从而$y=5,6$，进而解得$$(x,y,z)=(5,5,10).$$情形四 若$x=6$，则$\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{3}$，即$(y-3)(z-3)=9$，解得$$(x,y,z)=(6,6,6). $$
10．B．
不妨假设$a_1>a_2>\cdots>a_n$．若集合$A$中的正数的个数大于等于$4$，由于$a_2+a_3$和$a_2+a_4$均大于$a_2$，于是有$$a_2+a_3=a_2+a_4=a_1,$$所以$a_3=a_4$，矛盾．所以集合$A$中至多有$3$个正数．同理可知集合$A$中至多有$3$个负数．取$A=\left\{3,2,1,0,-1,-2,-3\right\}$，满足题意，所以$n$的最大值为$7$．
11．BD．
令$x=\tan{\alpha}$，$y=\tan{\beta}$，$z=\tan{\gamma}$，则
$$\dfrac{y-x}{1+xy}=\dfrac{z-y}{1+yz}=\dfrac{x-z}{1+zx}=\sqrt{3},$$
所以$$y-x=\sqrt{3}\left(1+xy\right),z-y=\sqrt{3}\left(1+yz\right),x-z=\sqrt{3}\left(1+zx\right),$$以上三式相加，即有$$xy+yz+zx=-3.$$
类似的，有$$\dfrac 1x-\dfrac 1y=\sqrt 3\left(\dfrac 1{xy}+1\right),\dfrac 1y-\dfrac 1z=\sqrt 3\left(\dfrac 1{yz}+1\right),\dfrac 1z-\dfrac 1x=\sqrt 3\left(\dfrac 1{zx}+1\right),$$以上三式相加，即有$$\dfrac 1{xy}+\dfrac 1{yz}+\dfrac 1{zx}=\dfrac{x+y+z}{xyz}=-3.$$
12．B．
设函数$f(x)=\sqrt{4x+1}$的图象，则其导函数$$f'(x)=\dfrac{2}{\sqrt{4x+1}}.$$作出函数$f(x)$的图象，函数$f(x)$的图象在$x=\dfrac 13$处的切线$y=\dfrac{2\sqrt{21}}7\left(x-\dfrac 13\right)+\dfrac{\sqrt{21}}3$，以及函数$f(x)$的图象过点$\left(-\dfrac 14,0\right)$和$\left(\dfrac 32,\sqrt 7\right)$的割线$y=\dfrac{4}{\sqrt 7}x+\dfrac{1}{\sqrt 7}$，如图．
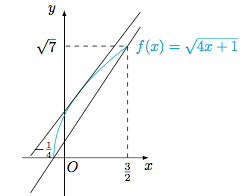于是可得$$\dfrac{4}{\sqrt 7}x+\dfrac{1}{\sqrt 7}\leqslant \sqrt{4x+1}\leqslant \dfrac{2\sqrt{21}}7\left(x-\dfrac 13\right)+\dfrac{\sqrt{21}}3,$$左侧等号当$x=-\dfrac 14$或$x=\dfrac 32$时取得；右侧等号当$x=\dfrac 13$时取得．因此原式的最大值为$\sqrt{21}$，当$a=b=c=\dfrac 13$时取得；最小值为$\sqrt{7}$，当$a=b=-\dfrac 14$，$c=\dfrac 32$时取得．从而原式最大值与最小值的乘积为$7\sqrt{3}=\sqrt{147}\in(\sqrt{144},\sqrt{169})$．
13．ABD．
由$x+y+z=1,\ x^2+y^2+z^2=1$，可知$xy+yz+zx=0$．设$xyz=c$，则$x,y,z$是关于$t$的方程$$t^3-t^2-c=0$$的三个实根．令$f(t)=t^3-t^2-c$，利用导数可得$$\begin{cases}f\left(0\right)=-c\geqslant 0,\\f\left(\dfrac{2}{3}\right)=-\dfrac{4}{27}-c\leqslant 0,\end{cases}$$所以$-\dfrac{4}{27}\leqslant c=xyz \leqslant 0$，等号显然可以取到．故选项A，B都对．因为$$(x+y)^2=(1-z)^2\leqslant 2\left(x^2+y^2\right)=2\left(1-z^2\right),$$所以$-\dfrac{1}{3}\leqslant z \leqslant 1$，等号显然可以取到．故选项C错，选项D对．
14．ACD．
因为\[\begin{split}a_{n+2}^2-a_{n+3}a_{n+1}&=a_{n+2}^2-\left(6a_{n+2}-a_{n+1}\right)a_{n+1}\\&=a_{n+2}^2-6a_{n+2}a_{n+1}+a_{n+1}^2\\&=a_{n+2}\left(a_{n+2}-6a_{n+1}\right)+a_{n+1}^2\\&=a_{n+1}^2-a_{n+2}a_{n}, \end{split}\]所以A正确．
由于$a_3=11$，故\[\begin{split}a_{n+1}^2-a_{n+2}a_{n}&=a_{n+1}^2-\left(6a_{n+1}-a_n\right)a_{n}\\&=a_{n+1}^2-6a_{n+1}a_{n}+a_{n}^2\\&=-7\end{split}\]
对任意正整数恒成立，所以$4a_na_{n+1}-7=\left(a_{n+1}-a_{n}\right)^2$，$8a_na_{n+1}-7=\left(a_{n+1}+a_{n}\right)^2$，故C, D正确．
计算前几个数即可判断B错误．
注 若数列$\left\{a_n\right\}$满足$a_{n+2}=pa_{n+1}-a_{n}\left(n\in\mathbf{N}^{*}\right)$，则$a_{n+1}^2-a_{n+2}a_{n}$为定值．
15．CD．
因为$$\left||z|-\dfrac{1}{|z|}\right|\leqslant\left|z+\dfrac{1}{z}\right|=1,$$故$\dfrac{\sqrt{5}-1}{2}\leqslant |z|\leqslant\dfrac{\sqrt{5}+1}{2}$，等号分别当$z=\dfrac{\sqrt 5+1}2{\rm i}$和$z=\dfrac{\sqrt 5-1}2{\rm i}$时取得．
16．C．
从$2016$的约数中去掉$1,2$，其余的约数均可作为正多边形的边数．设从$2016$个顶点中选出$k$个构成正多边形，这样的正多边形有$\dfrac{2016}k$个，因此所求的正多边形的个数就是$2016$的所有约数之和减去$2016$和$1008$．考虑到$2016=2^5\cdot 3^2\cdot 7$，因此所求正多边形的个数为\[(1+2+4+8+16+32)\cdot (1+3+9)\cdot (1+7)-2016-1008=3528.\]
17．C．
设$P$点坐标为$\left(x_0,y_0\right)$，可得\[M\left(\dfrac{1}{2}x_0+y_0,\dfrac{1}{4}x_0+\dfrac{1}{2}y_0\right),\ N\left(\dfrac{1}{2}x_0-y_0,-\dfrac{1}{4}x_0+\dfrac{1}{2}y_0\right),\]故\[|MN|=\sqrt{\dfrac{1}{4}x_0^2+4y_0^2}\]为定值，所以
\[\dfrac{a^2}{b^2}=\dfrac{4}{\dfrac{1}{4}}=16,\]故$\sqrt{\dfrac ab}=2$．
注 (1) 若将两条直线的方程改为$y=\pm kx$，则$\sqrt{\dfrac{a}{b}}=\dfrac{1}{k}$；
(2) 两条相交直线上各取一点$M,N$，使得$|MN|$为定值，则线段$MN$中点$Q$的轨迹为圆或者椭圆．
18．B．
方程两边同时模$3$，可得$x^2\equiv 2^y \pmod 3$．因为$3 \nmid 2^y$，故$3 \nmid x^2$，所以\[x^2\equiv 1\pmod 3,\]故\[2^y\equiv 1\pmod 3,\]所以$y$是偶数．设$y=2m \left(m\in \mathbf{N}^{*}\right)$，则\[\left(2^m-x\right)\left(2^m+x\right)=615=3\cdot 5\cdot 41,\]解得$\begin{cases}2^m-x=5,\\2^m+x=123,\end{cases}$即$\begin{cases}x=59,\\y=12.\end{cases}$
19．AB．
根据卡特兰数的定义，可得$$I_n=C_{n-1}\cdot {\rm A}_n^n = \dfrac{1}{n}\cdot{\rm C}_{2n-2}^{n-1}\cdot n!=(n-1)!\cdot {\rm C}_{2n-2}^{n-1}.$$关于卡特兰数的相关知识见卡特兰数——计数映射方法的伟大胜利．
20．$0.165$．
根据概率的乘法公式，所求概率为$$0.3\cdot \left(0.5\cdot 0.3+0.5\cdot 0.8\right)=0.165.$$
21．$\dfrac{\sqrt{3}}{2}$．
当$x\to +\infty$时，$CP$趋于与平面$ABC$垂直，所求极限为$\triangle ABC$中$AB$边上的高，为$\dfrac{\sqrt 3}2$．
22．$\dfrac{1}{96}$．如图．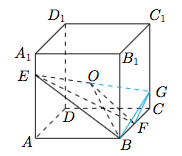
有$$V_{OEBF}=V_{O-EBF}=\dfrac 12\cdot V_{G-EBF}=\dfrac 12\cdot V_{E-GBF}=\dfrac 12\cdot \dfrac{1}{16}V_{E-BCC_1B_1}=\dfrac{1}{96}.$$
23．$0$．
根据题意，有$$\int_{0}^{2\pi}\left(x-\pi\right)^{2n-1}\left(1+\sin^{2n}{x}\right){\rm d}x=\int_{-\pi}^{\pi}x^{2n-1}\left(1+\sin^{2n}x\right){\rm d}x=0.$$
24．$1$．
根据题意，有$$\left(x^2+y^2\right)^3=4x^2y^2\leqslant \left(x^2+y^2\right)^2,$$于是$x^2+y^2\leqslant 1$，等号当$x^2=y^2=\dfrac 12$时取得，因此所求的最大值为$1$．
25．$\dfrac{3}{2}$，$\dfrac{\sqrt{22}-3}{2}$．
由柯西不等式可知，当且仅当$(x,y,z)=\left(1,\dfrac{1}{2},0\right)$时，$x+y+z$取到最大值$\dfrac{3}{2}$．
根据题意，有$$x^2+y^2+z^2+x+2y+3z=\dfrac{13}4,$$于是$$\dfrac{13}4\leqslant (x+y+z)^2+3(x+y+z),$$解得$$x+y+z\geqslant \dfrac{\sqrt {22}-3}2,$$于是$x+y+z$的最小值当$(x,y,z)=\left(0,0,\dfrac{\sqrt{22}-3}{2}\right)$时取得，为$\dfrac{\sqrt{22}-3}{2}$．
26．$\dfrac 23$．
根据奔驰定理，有$$\lambda+\mu=\dfrac{2}{9}+\dfrac{4}{9}=\dfrac{2}{3}.$$
27．$\cos\dfrac{5\pi}3+{\rm i}\sin\dfrac{5\pi}3$．
根据题意，有$$z^3+\dfrac{z^2}{z^2+z+2}=1+z^2=-z=\cos\dfrac{5\pi}3+{\rm i}\sin\dfrac{5\pi}3.$$
28．$\dfrac{200\pi}3+100\sqrt 3-300$．
设$z=x+y{\rm i}$，其中$x,y\in\mathbf R$．由于$\dfrac{40}{\bar z}=\dfrac{40z}{|z|^2}$，于是$$\begin{cases} \dfrac x{10}\geqslant 1,\dfrac y{10}\geqslant 1,\\ \dfrac{40x}{x^2+y^2}\geqslant 1,\dfrac{40y}{x^2+y^2}\geqslant 1,\end{cases} $$如图．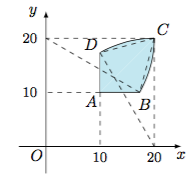
弓形面积为$$\dfrac 12\cdot 20^2\cdot \left(\dfrac{\pi}6-\sin\dfrac{\pi}6\right)=\dfrac{100\pi}3-100,$$四边形$ABCD$的面积为$$2\cdot\dfrac 12\left(10\sqrt 3-10\right)\cdot 10=100\sqrt 3-100,$$于是所求面积为$$2\left(\dfrac{100\pi}3-100\right)+\left(100\sqrt 3-100\right)=\dfrac{200\pi}3+100\sqrt 3-300.$$
29．$\sqrt 3$．
根据题意，有\[\begin{split}&\dfrac{\sin{4x}}{\cos{8x}\cos{4x}}+\dfrac{\sin{2x}}{\cos{4x}\cos{2x}}+\dfrac{\sin{x}}{\cos{2x}\cos{x}}+\dfrac{\sin{x}}{\cos{x}}\\=&(\tan{8x}-\tan{4x})+(\tan{4x}-\tan{2x})+(\tan{2x}-\tan{x})+\tan{x}\\=&\tan{8x}\\=&\sqrt{3}.\end{split}\]
30．$441000$．
首先确定偶数的位置有多少种选择．
第一行两个偶数有$\mathrm{C}_{4}^{2}$种选择，下面考虑这两个偶数所在的列，每列还需再填一个偶数，设为$a,b$．
情形一 若$a,b$位于同一行，它们的位置有$3$种选择，此时剩下的四个偶数所填的位置唯一确定．
情形二 若$a,b$位于不同的两行，它们的位置有$6$种选择，此时剩下的四个偶数所填的位置有$2$种选择．
所以偶数的不同位置数为$$\mathrm{C}_{4}^{2}\cdot \left(3+6\cdot 2\right)=90,$$因此总的填法数位$$90\cdot\mathrm{C}_{8}^{4}\cdot\mathrm{C}_{8}^{4}=441000.$$
31．$8$．
一方面，设$A=\left\{a_1,a_2,\cdots,a_k\right\}$，其中$k\in \mathbf{N}^{*}$，$1\leqslant k \leqslant 14$．不妨假设$a_1<a_2<\cdots<a_{k}$．若$k \geqslant 9$，由题意，$a_3-a_1\geqslant 3$，$a_5-a_3\geqslant 3$，且$a_5-a_3\ne a_3-a_1$，故$$a_5-a_1\geqslant 7,$$同理，$a_9-a_5\geqslant 7$，又因为$a_9-a_5\ne a_5-a_1$，所以$a_9-a_1\geqslant 15$，矛盾．故$k \leqslant 8$．
另一方面，取$A= \left\{1,2,4,5,10,11,13,14\right\}$，满足题意．
综上所述，$A$中元素个数的最大值为$8$．