2016年北大全国优秀中学生暑期学堂数学试题

文科生做前5题，理科生做后5题，每题20分．

1．设关于$x$的方程$\sin^2 x+\cos x+a=0$在实数范围内有解，求实数$a$的取值范围．

2．设$a,b,c$均为正数且$a,b,c$成等差数列，判断$\dfrac 1{\sqrt b+\sqrt c},\dfrac 1{\sqrt c+\sqrt a},\dfrac 1{\sqrt a+\sqrt b}$是否成等差数列，并说明理由．

3．设$a,b,c$为实数，证明：对任意实数$x$都有$(x-a)^2+(x-b)^2\geqslant c$当且仅当$(a-b)^2\geqslant 2c$．

4．已知复数$z_1,z_2$满足$z_1$与$z_1+z_2$有相同的模且$\overline{z_1}z_2=a(1-\rm i)$，其中$a$为非零实数，求$\dfrac{z_2}{z_1}$的值．

5．一条直线与双曲线交于$A,B$两点，与此双曲线的渐近线交于$C,D$两点，证明：线段$AC$与$BD$的长度相等．

6．设$\alpha,\beta$均为锐角，满足$\sin^2 \alpha+\sin^2 \beta=\sin(\alpha+\beta)$，求$\alpha+\beta$的值．

7．已知$\triangle ABC$的面积为$1$，$D,E$分别是边$AB,AC$上的点，$F$为线段$DE$上的一点，设$AD:AB=x,\ AE:AC=y,\ DF:DE=z$且$y+z-x=1$．求$\triangle BDF$的面积的最大值并求出此时$x,y,z$的值．

---

 

参考答案

1．题中方程有解即$a=-\sin^{2}x-\cos x$有解，从而有

$$a=\cos^{2}x-\cos x-1=\left(\cos x-\dfrac 12\right )^{2}-\dfrac 54\in\left[-\dfrac 54,1\right].$$

2．由题意知$b-a=c-b=\dfrac 12(c-a)$，所以

$$\dfrac {1}{\sqrt b+\sqrt c}+\dfrac 1{\sqrt a+\sqrt b}=\dfrac {\sqrt c-\sqrt b}{c-b}+\dfrac {\sqrt b-\sqrt a}{b-a}=\dfrac {\sqrt c-\sqrt a}{b-a}=\dfrac {\sqrt c-\sqrt a}{\frac 12(c-a)}=\dfrac {2}{\sqrt c+\sqrt a}.$$ 从而得到$\dfrac 1{\sqrt b+\sqrt c},\dfrac 1{\sqrt c+\sqrt a},\dfrac 1{\sqrt a+\sqrt b}$是等差数列．

3．对题中不等式整理得

$$2x^{2}-2(a+b)x+(a^{2}+b^{2}-c)\geqslant 0,$$ 此不等式恒成立当且仅当对应判别式 $$\Delta =4(a+b)^{2}-8(a^{2}+b^{2}-c)=4[2c-(a-b)^{2}]\leqslant 0,$$ 等价于$2c\leqslant (a-b)^{2}$，命题得证．

4．由题意知

$$|z_{1}|^2=z_1\overline{z_1}=|z_1+z_2|^2=(z_1+z_2)(\overline{z_1}+\overline{z_2}),$$ 化简得 $$z_2\overline{z_2}+z_2\overline{z_1}+z_1\overline{z_2}=0.$$ 因为$\overline{z_1}z_2=a(1-{\rm i})$，所以$z_1\overline{z_2}=a(1+{\rm i})$，代入上面的式子得$z_2\overline{z_2}=-2a$．于是有 $$\dfrac {z_2}{z_1}=\dfrac {z_2\overline{z_2}}{z_1\overline{z_2}}=\dfrac {-2a}{a(1+{\rm i})}=-1+{\rm i}.$$

5．以双曲线的中心为原点，以实轴所在直线为$x$轴建立直角坐标系，则双曲线与它的渐近线方程可以表示为

$$\dfrac {x^2}{a^2}-\dfrac {y^2}{b^2}=\lambda,$$ 其中$\lambda=1$时为双曲线，$\lambda=0$时为渐近线．
设$A(x_1,y_1),B(x_2,y_2),C(x_3,y_3),D(x_4,y_4)$，则有 $$\begin{cases} \dfrac {x_1^2}{a^2}-\dfrac {y_1^2}{b^2}=1,\\\dfrac {x_2^2}{a^2}-\dfrac {y_2^2}{b^2}=1,\end{cases}$$ 两式相减得 $$\dfrac{(x_1-x_2)(x_1+x_2)}{a^2}-\dfrac {(y_1-y_2)(y_1+y_2)}{b^2}=0,$$ 同样有 $$\dfrac{(x_3-x_4)(x_3+x_4)}{a^2}-\dfrac {(y_3-y_4)(y_3+y_4)}{b^2}=0,$$ 因为$A,B,C,D$四点共线，当此直线斜率不存在或者斜率为零时，由双曲线的对称性得$AC=BD$；当此直线的斜率$k$存在且不为零时，有 $$\dfrac {y_1+y_2}{x_1+x_2}=\dfrac {y_3+y_4}{x_3+x_4}=\dfrac {b^2}{a^2k},$$ 即$AB$的中点与$CD$的中点在过原点的同一条直线上，所以它们重合，从而有$AC=BD$．
事实上，此结论可以直接由双曲线的“垂径定理”得到．

6．显然当$\alpha +\beta =\dfrac {\pi}{2}$时，等式成立；
由已知条件知

$$\sin^2\alpha +\sin^2\beta=\sin\alpha \cos\beta+\cos\alpha \sin\beta,$$ 整理得 $$\sin\alpha (\sin\alpha -\cos\beta)=\sin\beta(\cos\alpha -\sin\beta).$$ 若$\alpha +\beta\ne\dfrac {\pi}{2}$，则有$\sin\alpha-\cos\beta$与$\cos\alpha-\sin\beta$同号．
若它们同为正，则有 $$\sin\alpha>\cos\beta=\sin\left(\dfrac {\pi}{2}-\beta\right ),\cos\alpha =\sin\left(\dfrac {\pi}{2}-\alpha \right )>\sin\beta,$$ 从而有 $$\alpha >\dfrac {\pi}{2}-\beta,\dfrac {\pi}{2}-\alpha >\beta,$$ 无解；
若它们同为负，用类似的方式也可以推导出矛盾．
综上，$\alpha +\beta=\dfrac {\pi}{2}$．

7．如图，连结$BE$：
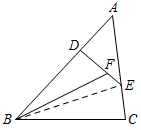由三角形的面积公式$S=\dfrac 12ab\sin C$可以得到

$$S_{\triangle ADE}=xyS_{\triangle ABC}=xy,S_{\triangle BCE}=(1-y)S_{\triangle ABC}=1-y,$$ 所以有 $$S_{\triangle BDE}=1-xy-(1-y)=y(1-x).$$ 从而有 $$S_{\triangle BDF}=zS_{\triangle BDE}=zy(1-x)\leqslant \left(\dfrac {z+y+1-x}{3}\right )^3=\dfrac {8}{27}.$$ 当$y=z=1-x$时，即$x=\dfrac 13,y=z=\dfrac 23$时等号成立，此时$\triangle BDF$的面积有最大值$\dfrac {8}{27}$．

---

点击此处下载pdf．