题目原出处:http://blog.sina.com.cn/s/blog_4c1131020102wjf5.html
一、填空题
1、设函数$f(x)=\sin\left(\omega x+\varphi\right)$($\omega \ne 0$)的图象关于直线$x=-1$和直线$x=2$均对称,则$f(0)$的所有可能取值是_______.
2、方程$x^3-2ax+a^2=0$有在区间$(0,1)$内的实数解,则$a$的取值范围是_______.
3、设复数$z$满足$|z|=2$,${\rm i}$是虚数单位,则$\left|(1+z)+{\rm i}(1-z)\right|$的最大值是_______.
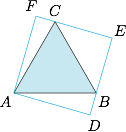
4、设边长为$1$的正三角形可被边长为$b$的正方形覆盖,则$b$的最小值是_______.
5、在四面体$ABCD$中,$AD=BD=CD$,$AB=BC=CA=1$.若二面角$A-BC-D$等于$75^\circ$,则二面角$A-BD-C$的余弦值是_______.
6、在平面直角坐标系中,$\triangle ABC$是边长为$1$的正三角形.动点$P$满足$\overrightarrow{PA}\cdot \overrightarrow{PB}+\overrightarrow{PB}\cdot \overrightarrow{PC}+\overrightarrow{PC}\cdot \overrightarrow{PA}=0$,则$P$的轨迹所围成的平面区域的面积是_______.
7、化简$\displaystyle\sum_{k=0}^{1008}(-1)^k{\rm C}_{2016}^{2k}=$_______.
8、设随机变量$X$服从正态分布$N(1,1)$,若$P(|X|>1)=c$,则$P(X<2)=$_______.
二、解答题
9、设正数$a,b,c$满足$ab+bc+ca=1$,求$\dfrac{a}{\sqrt{1+a^2}}+\dfrac{b}{\sqrt{1+b^2}}+\dfrac{c}{\sqrt{1+c^2}}$的取值范围.
10、过椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的右焦点$F$作两条相互垂直的弦$AB,CD$,证明:$A,B,C,D$四点共圆当且仅当$|AB|=|CD|$.
11、袋中共有$3n$个小球,红、绿、蓝各$n$个.现从袋中随机取球,每次取出$3$个小球不放回,直至某种颜色的小球被全部取出,求取球次数$X$的分布列.
12、设$f(x)={\rm e}^x-\cos x$,正项数列$\{a_n\}$满足$a_1=1$,$f(a_n)=a_{n-1}$,$n\geqslant 2$.证明:存在正整数$n$使得$\displaystyle \sum_{k=1}^{n}a_k>2016$.
参考答案
一、填空题
1、$\pm 1,\pm \dfrac 12$
根据题意,$3$是半周期的整数倍,于是$\omega = \dfrac{k\pi}{3}$($k\in\mathbb Z,k\ne 0$),因此$$f(0)=\sin \varphi =\sin (-\omega +\varphi+\omega)=\sin (-\omega+\varphi)\cos \omega+\cos(-\omega+\varphi)\sin \omega=\pm \cos\omega,$$于是$f(0)$的所有可能取值是$\pm 1,\pm \dfrac 12$.
2、$\left(0,\dfrac{32}{27}\right]$
根据题意,有$a=x\left(1 \pm \sqrt{1-x}\right)$($x\in (0,1)$),设$1-x=(t-1)^2$,$t\in (0,1)\cup (1,2)$,则$$0<a=t^2(2-t)=\dfrac{t\cdot t\cdot (4-2t)}2\leqslant \dfrac 12\left(\dfrac 43\right)^3=\dfrac{32}{27},$$当$t=1$时,$a=1$,经检验$a=1$时满足条件,结合连续性可得$a$的取值范围是$\left(0,\dfrac{32}{27}\right]$.
3、设$z=a+b{\rm i}$,则\[\begin{split} \left|(1+z)+{\rm i}(1-z)\right|&=\left|(1+a+b)+(1-a+b){\rm i}\right|\\
&=\sqrt{(1+a+b)^2+(1-a+b)^2}\\
&=\sqrt{10+4b}\\
&\leqslant 3\sqrt 2,\end{split} \]等号当$b=2$,即$z=2{\rm i}$时取得.因此所求的最大值为$3\sqrt 2$.
另法 由题意得\[\begin{split}\left|(1+z)+{\rm i}(1-z)\right|=&\left|(1+{\rm i})+(1-{\rm i})z\right|\\=&|1-{\rm i}|\cdot |z+{\rm i}|=\sqrt 2\cdot|z+{\rm i}|\\\leqslant&{\sqrt 2}\cdot(|z|+|{\rm i}|)=3\sqrt 2.\end{split}\]当$z=2{\rm i}$时取到等号.
4、$\dfrac{\sqrt 6+\sqrt 2}4$
想象一个大矩形将边长为$1$的正三角形覆盖,然后保持矩形的长和宽的方向不变缩小矩形,直至矩形的边碰到正三角形的三个顶点.此时必有一个顶点与矩形的顶点重合,如图.
设$\angle BAD=\alpha$,$\angle CAF=\beta$,则$\alpha+\beta=30^\circ$,且此方向上的正方形(由矩形补成)边长的最小值为$$\max\{\cos\alpha,\cos\beta\}\geqslant \cos 15^\circ=\dfrac{\sqrt 6+\sqrt 2}4,$$等号当$\alpha=\beta=15^\circ$时取得.因此所求的最小值为$\dfrac{\sqrt 6+\sqrt 2}4$.
5、设$\angle DAB=\theta$,$A-BD-C$的大小为$\varphi$,则根据三面角定理,有$$\cos\angle ABD=\cos\angle CBA\cdot\cos\angle DBC+\sin\angle CBA\cdot\sin\angle DBC\cdot\cos 75^\circ,$$即$$\cos\theta=\dfrac 12\cos\theta+\dfrac{\sqrt 3}2\sin\theta\cdot\cos 75^\circ,$$从而$\dfrac{\cos\theta}{\sin\theta}=\sqrt 3\cos 75^\circ$,又$$\cos\angle ABC=\cos\angle ABD\cdot\cos\angle CBD+\sin\angle ABD\cdot\sin\angle CBD\cdot\cos\varphi,$$即$$\dfrac 12=\cos^2\theta+\sin^2\theta\cdot \cos\varphi,$$从而$$\cos\varphi=\dfrac{1-2\cos^2\theta}{2\sin^2\theta}=\dfrac{\sin^2\theta-\cos^2\theta}{2\sin^2\theta}=\dfrac 12-\dfrac 32\cos^2 75^\circ=\dfrac{3\sqrt 3-2}8.$$
6、$\dfrac{\pi}6$
设$P(x,y)$,$A\left(-\dfrac 12,0\right)$,$B\left(\dfrac 12,0\right)$,$C\left(0,\dfrac{\sqrt 3}2\right)$,则根据题意有$$\left(-\dfrac 12-x\right)\left(\dfrac 12-x\right)+y^2+\left(\dfrac 12-x\right)(-x)+(-y)\left(\dfrac{\sqrt 3}2-y\right)+(-x)\left(-\dfrac 12-x\right)+(-y)\left(\dfrac{\sqrt 3}2-y\right)=0,$$整理得$$x^2+\left(y-\dfrac{\sqrt 3}6\right)^2=\dfrac 16,$$因此所求面积为$\dfrac{\pi}6$.
7、$2^{1008}$
原式即$\left(1+{\rm i}\right)^{2016}$的实部,而$$\left(1+{\rm i}\right)^{2016}=\left[\sqrt 2\cdot \left(\cos \dfrac{\pi}4+{\rm i}\sin\dfrac{\pi}4\right)\right]^{2016}=2^{1008}\left(\cos 504\pi+{\rm i}\sin 504\pi\right)=2^{1008},$$因此原式的值为$2^{1008}$.
8、题应有误,尚待核实
二、解答题
9、设$a=\tan\dfrac A2,b=\tan\dfrac B2,c=\tan\dfrac C2$,其中$A+B+C=\pi$,$A,B,C>0$,则$$\dfrac{a}{\sqrt{1+a^2}}+\dfrac{b}{\sqrt{1+b^2}}+\dfrac{c}{\sqrt{1+c^2}}=\sin\dfrac A2+\sin\dfrac B2+\sin\dfrac C2.$$一方面,有$$\sin\dfrac A2+\sin\dfrac B2+\sin\dfrac C2\leqslant 3\sin\dfrac{A+B+C}6=\dfrac 32,$$等号当$A=B=C=\dfrac{\pi}3$时取得;另一方面,有$$\sin\dfrac A2+\sin\dfrac B2+\sin\dfrac C2>\sin\dfrac{A+B}2+\sin\dfrac C2>\sin\dfrac{A+B+C}2=1,$$当$(A,B,C)\to (0,0,\pi)$时,$\sin\dfrac A2+\sin\dfrac B2+\sin\dfrac C2\to 1$.于是所求的取值范围是$\left(1,\dfrac 32\right]$.
10、我们熟知已知二次曲线上四点$A,B,C,D$,若$AB,CD$斜率均存在,则$AB$与$CD$的斜率互为相反数与$A,B,C,D$四点共圆等价.结合椭圆的对称性,原命题成立.
注 考虑非圆二次曲线$Ax^2+By^2+Dx+Ey+F=0$($A\neq B$)与两条相交直线$(y-k_1x-b_1)\cdot (y-k_2x-b_2)=0$($k_1\neq k_2$)形成的交点曲线系$$Ax^2+By^2+Dx+Ey+F-\lambda\cdot (y-k_1x-b_1)(y-k_2x-b_2)=0,$$当且仅当$k_1+k_2=0$时该方程表示圆,因此引理得证.
11、我还没做出来
12、函数$f(x)$的导函数$f'(x)={\rm e}^x+\sin x$,于是函数$f(x)$在$(0,+\infty)$上单调递增.猜测$a_n\geqslant \dfrac 1n$,等号当且仅当$n=1$时成立.用数学归纳法证明如下.
当$n=1$时,命题显然成立;
假设当$n=k$时命题成立,即$a_k\geqslant \dfrac 1k$,则$${\rm e}^{a_{k+1}}-\cos a_{k+1}=a_k\geqslant \dfrac 1k.$$考虑函数$h(x)=f(x)-\dfrac{x}{1-x}$,$x\in (0,1)$.我们熟知当$x \in (0,1)$时,有$$\cos x>1-\dfrac 12x^2,{\rm e}^x<-1+\dfrac{4}{2-x},$$于是$$h(x)<-1+\dfrac{4}{2-x}-1+\dfrac 12x^2-\dfrac{x}{1-x}=\dfrac{x^3(x-3)}{2(2-x)(1-x)}<0.$$令$x=\dfrac{1}{k+1}$,则有$${\rm e}^{\frac{1}{k+1}}-\cos\dfrac{1}{k+1}-\dfrac 1k<0,\ \text{即}\ f\left(\dfrac{1}{k+1}\right)<{\rm e}^{a_{k+1}}-\cos a_{k+1},$$结合$f(x)$在$(0,+\infty)$上单调递增,有$a_{k+1}>\dfrac{1}{k+1}$.
综上所述,猜测得证.于是当$n\geqslant 2^m$($m\in\mathbb N^*$)时,有\[\begin{split} \sum_{k=1}^{n}a_k&>1+\dfrac 12+\dfrac 13+\dfrac 14+\dfrac 15+\dfrac 16+\dfrac 17+\dfrac 18+\cdots +\dfrac 1n\\
&\geqslant 1+\dfrac 12+\dfrac 14+\dfrac 14+\dfrac 18+\dfrac 18+\dfrac 18+\dfrac 18+\cdots +\dfrac{1}{2^m}+\dfrac{1}{2^m}+\cdots +\dfrac{1}{2^m}\\
&=\dfrac{m+2}2,\end{split} \]因此取$m=4030$,$n=2^{4030}$时,$\displaystyle \sum_{k=1}^{n}a_k>2016$.