问题从2014年北京市朝阳区高三期中考试理科数学第14题(填空压轴题)开始:
已知函数\(f(x)=a^x\)(\(0<a<1\)),数列\(\left\{a_n\right\}\)满足\(a_1=f(1)\),\(a_{n+1}=f\left(a_n\right)\),\(n\in\mathcal N^*\),则\(a_2\)与\(a_3\)中,较大的是________;\(a_{20},a_{25},a_{30}\)的大小关系是_______.
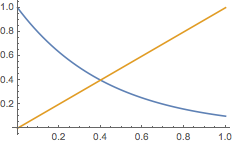
本题应用迭代函数法(可以参考:每日一题[182] 迭代函数法 以及 每日一题[195] 迭代函数法 .)解决并不困难,在直角坐标平面上作出迭代函数\(f(x)=a^x\)的图象与直线\(y=x\)可得数列\(\left\{a_n\right\}\)的子列\(\left\{a_{2n-1}\right\}\)单调递增有上界\(x_0\),子列\(\left\{a_{2n}\right\}\)单调递减有下界\(x_0\),其中\(x_0\)为不动点方程\[a^x=x\]的唯一实根.因此答案为\(a_2>a_3\),\(a_{20}>a_{30}>a_{25}\).
很明显,数列\(\left\{a_n\right\}\)的子列\(\left\{a_{2n-1}\right\}\)和子列\(\left\{a_{2n}\right\}\)均有极限,这个极限一定是\(x_0\)吗?
为此,我们要研究\(f(x)\)的二阶不动点方程\[a^x={\log_a}x,\]其中\(0<a<1\).
事实上,\(f(x)\)的一阶不动点\(x_0\)一定是其二阶不动点.现在假设存在非一阶不动点的二阶不动点\(x_1\)、\(x_2\),则\[a^{x_1}=x_2\land a^{x_2}=x_1,\]于是\[\ln a=\dfrac{\ln x_2}{x_1}=\dfrac{\ln x_1}{x_2},\]从而\[x_1\ln x_1=x_2\ln x_2.\]
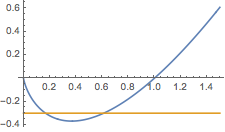
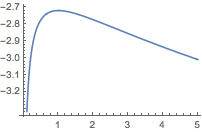
如图,假设\(y=m\)与\(y=x\ln x\)的图象交于两点,交点横坐标分别为\(x_1\)、\(x_2\),其中\(x_1<x_2\),\(-\dfrac 1{\rm e}<m<0\).记\(t=\dfrac{x_2}{x_1}\),则不难得到\[\ln x_1=\dfrac{t\ln t}{1-t},\ln x_2=\dfrac{\ln t}{1-t},\]于是\[\ln a=t^{\frac{1}{t-1}}\cdot \dfrac{t\ln t}{1-t},\]记右侧函数为$\varphi(t)$,则其导函数\[\varphi'(t)=t^{\frac{t}{t-1}}\cdot \dfrac{\ln t+\left(\sqrt t-\dfrac{1}{\sqrt t}\right)}{(t-1)^3}\cdot \left[\ln t-\left(\sqrt t-\dfrac{1}{\sqrt t}\right)\right],\]又考虑到\[\lim_{t\to 1}t^{\frac{1}{t-1}}\cdot \dfrac{t\ln t}{1-t}=-{\rm e},\]
于是当\(0<a<\left(\dfrac 1{\rm e}\right)^{\rm e}\)时,函数\(f(x)=a^x\)有三个二阶不动点,且满足\[a<x_1<\dfrac 1{\rm e}<x_2<1,\] 这里用到了\[\dfrac{\ln a}{\ln x_1}=\dfrac 1{x_2}>1.\]
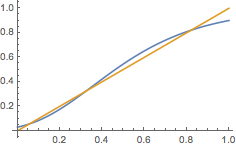
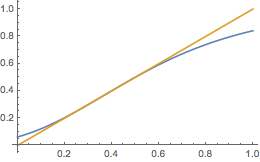
设\(a_0=1\),则当\(0<a<\left(\dfrac 1{\rm e}\right)^{\rm e}\)时,由迭代函数的图象与直线\(y=x\)可得子列\(\left\{a_{2n-1}\right\}\)单调递增极限为\(x_1\),子列\(\left\{a_{2n}\right\}\)单调递减极限为\(x_2\).(图中为\(a=0.03\)的情形)
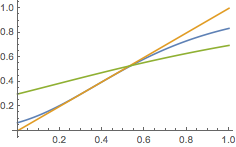
当\(\left(\dfrac 1{\rm e}\right)^{\rm e}\leqslant a<1\)时,由迭代函数的图象与直线\(y=x\)可得子列\(\left\{a_{2n-1}\right\}\)单调递增极限为\(x_0\),子列\(\left\{a_{2n}\right\}\)单调递减极限为\(x_0\).(图中分别为\(a=\left(\dfrac 1{\rm e}\right)^{\rm e}\)和\(a=0.3\)的情形)
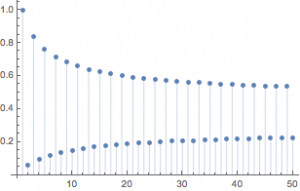
注 本题中的分界点是个很小的数\(\left(\dfrac 1{\rm e}\right)^{\rm e}\approx 0.0659880358\).在\(\left(0,\left(\dfrac 1{\rm e}\right)^{\rm e}\right)\)上取\(a=\dfrac 1{16}\),则可得\(f(x)=a^x\)的非一阶不动点的二阶不动点分别为\(x_1=\dfrac 14\)和\(x_2=\dfrac 12\).
此时数列的散点图如图.很明显两个子列的极限不同.