每日一题[195] 迭代函数法

2014年全国高中数学联赛河北省预赛第14题：

已知数列\(\left\{a_n\right\}\)满足：\(a_1=1\)，\(a_n=\dfrac{1}{a_{n+1}}-\dfrac 12\)．

（1）求证：\(a_n\geqslant \dfrac 23\)；

（2）求证：\(\left|a_{2n}-a_n\right|<\dfrac{10}{27}\)．

（1）证明    根据已知可得\(a_{n+1}=\dfrac{2}{2a_n+1}\)，设迭代函数\(f(x)=\dfrac{2}{2x+1}\)，则\(a_{n+1}=f\left(a_n\right)\)，如图．其中\(a_1=1\)，\(a_2=\dfrac 23\)．

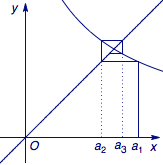
我们证明一个更强的结论：\[\dfrac 23\leqslant a_n\leqslant 1,\]用数学归纳法证明．

当\(n=1\)时，命题显然成立．

假设命题对\(n\)成立，则由函数\(f(x)\)在\(\left[\dfrac 23,1\right]\)上单调递减可得\[f\left(\dfrac 23\right)\geqslant f\left(a_n\right)\geqslant f(1),\]即\[\dfrac 23\leqslant a_{n+1}\leqslant \dfrac 67\leqslant 1,\]从而命题对\(n+1\)也成立．

综上，命题得证．

（2）证明    根据（1）中已经证明的加强的结论可得数列\(\left\{a_n\right\}\)中任意两项的差的绝对值不大于\(\dfrac 13\)，因此命题显然成立．

注    利用迭代函数的图象是研究数列的有界性以及单调性的重要方法，还可以参考每日一题[182] 不动点．下面给出两道练习题．

1、（2015年山西省预赛第10题）已知数列\(\{a_n\}\)，\(\{b_n\}\)满足条件：\(a_1=b_1=1\)，\(a_{n+1}=a_n+2b_n\)，\(b_{n+1}=a_n+b_n\)；证明：对每个正整数\(n\)，下式成立：

（1）\(\dfrac{a_{2n-1}}{b_{2n-1}}<\sqrt 2<\dfrac{a_{2n}}{b_{2n}}\)；

（2）\(\left|\dfrac{a_{n+1}}{b_{n+1}}-\sqrt 2\right|<\left|\dfrac{a_n}{b_n}-\sqrt 2\right|\)．

2、已知数列\(\{x_n\}\)满足\(x_1=\dfrac 12\)，\(x_{n+1}=\dfrac 1{1+x_n},n\in \mathcal {N}^*\)，证明：\(\left|x_{n+1}-x_n\right|\leqslant \dfrac 16\left(\dfrac 25\right)^{n-1}\)．