一组函数问题中的代数变形

函数是一种特殊的方程．对方程进行其当的代数变形，使得其中的一边获得优化，而另外一边不会因此变得无法进行下一步处理是我们应对方程的惯用方法．下面通过一组例题说明恰当的代数变形对解函数题的重要帮助．

• 第一题是2012年山东的选择最后一题：

设函数$f(x)=\dfrac 1x$，$g(x)=ax^2+bx(a,b\in\mathcal R,a\neq 0)$，若$y=f(x)$的图象与$y=g(x)$的图象有且仅有两个不同的公共点$A(x_1,y_1)$，$B(x_2,y_2)$，则下列判断正确的是（        ）

A．$a<0$时，$x_1+x_2<0$，$y_1+y_2>0$

B．$a<0$时，$x_1+x_2>0$，$y_1+y_2<0$

C．$a>0$时，$x_1+x_2<0$，$y_1+y_2<0$

D．$a>0$时，$x_1+x_2>0$，$y_1+y_2>0$

考虑方程

$$\dfrac 1x=ax^2+bx,$$ 将其变形为 $$\dfrac 1{x^2}=ax+b,$$ 则问题获得化简．

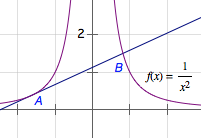
如图，$a<0$时，$x_1+x_2>0$，$y_1+y_2=\dfrac 1{x_1}+\dfrac 1{x_2}=\dfrac {x_1+x_2}{x_1x_2}<0$，故选B．

---

 

• 第二题是2014年江苏卷的23题：

已知函数$f_0(x)=\dfrac {\sin x}{x}(x>0)$．设$f_n(x)$为$f_{n-1}(x)$的导数，$n\in \mathcal N^*$．

(1) 求$2f_1\left(\dfrac {\pi}2\right)+\dfrac {\pi}2f_2\left(\dfrac {\pi}2\right)$的值；

(2) 证明：对任意的$n\in \mathcal N^*$，等式

$$\left|nf_{n-1}\left(\dfrac {\pi}4\right)+\dfrac {\pi}4f_n\left(\dfrac {\pi}4\right)\right|=\dfrac {\sqrt 2}2$$ 都成立．

这个题目的关键就是

$$\begin{split}xf_0(x)&=\sin x\\f_0(x)+xf_1(x)&=\cos x\\2f_1(x)+xf_2(x)&=-\sin x\\\cdots&\cdots\\nf_{n-1}(x)+xf_n(x)&=(\sin x)^{(n)}\end{split}.$$

---

 

•  最后我们看看2014年辽宁卷的最后一题：

已知函数

$$\begin{split}f(x)&=(\cos x-x)(\pi+2x)-\dfrac 83(\sin x+1),\\g(x)&=3(x-\pi)\cos x-4(1+\sin x)\ln\left(3-\dfrac {2x}{\pi}\right).\end{split}$$

证明：

(1) 存在唯一的$x_0\in\left(0,\dfrac {\pi}2\right)$，使$f(x_0)=0$；

(2) 存在唯一$x_1\in\left(\dfrac {\pi}2,\pi\right)$，使$g(x_1)=0$，且对(1)中的$x_0$，有$x_0+x_1<\pi$．

第1小题是很常规的问题．事实上，$f(0)>0>f\left(\dfrac {\pi}2\right)$，且当$x_0\in\left(0,\dfrac {\pi}2\right)$时，$f'(x)<0$．因此原命题得证．

对于第2小题，先做常规的换元$t=\pi-x$，则

$$g(t)=3t\cos t-4(1+\sin t)\ln\left(1+\dfrac {2t}{\pi}\right).$$

设该函数的零点为$t_0$，则问题转化为证明$x_0<t_0$．为了处理其中的对数函数，我们两边同除以一个恒正的代数式$1+\sin t$，而这样做并不会影响函数的零点位置．于是经过计算整理可得

$$\left(\dfrac {g(t)}{1+\sin t}\right)'=\dfrac {f(t)}{\dfrac 23(1+\sin t)\left(t+\dfrac {\pi}2\right)}.$$

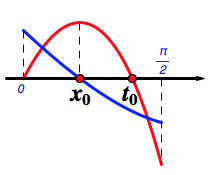
根据导函数图象画函数图象（注意到$g(0)=0$），于是原命题得证．