函数小题一则

这是2014年辽宁卷的第14小题：

已知函数\(f(x)=\left|x^2+3x\right|\)，若方程\(f(x)-a|x-1|=0\)恰有\(4\)个互异的实数根，则实数\(a\)的取值范围是________．

一般的想法是分离变量：

\[a=\frac{\left|x^2+3x\right|}{|x-1|},\]

令\(t=x-1\)可得\[a=\left|t+\frac 4t+5\right|.\]

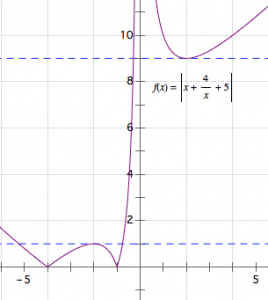
画图得\(a\)的取值范围是\((0,1)\cup(9,+\infty)\)．

事实上，直接代数求解更快：

显然\(a>0\)，根据题意

\[\begin{split}f(x)-a|x-1|=0&\Leftrightarrow x^2+3x=ax-a \lor x^2+3x=-ax+a\\&\Leftrightarrow x^2+(3-a)x+a=0 \lor x^2+(3+a)x-a=0.\end{split}\]

因此\[(3-a)^2-4a>0 \land (3+a)^2+4a>0 \Leftrightarrow a<1 \lor a>9.\]

注意到两个方程相加有\[2x^2+6x=0,\]于是不会有重根．

这样就得到了\(a\)的取值范围是\((0,1)\cup(9,+\infty)\)．

这个小题告诫我们，并不是任何函数的零点问题都是数形结合方法最优，多试探多总结才能更有所得．