平面直角坐标系$xOy$中,椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的离心率是$\dfrac{\sqrt 3}{2}$,抛物线$E:x^2=2y$的焦点$F$是$C$的一个顶点.
(1) 求椭圆$C$的方程;
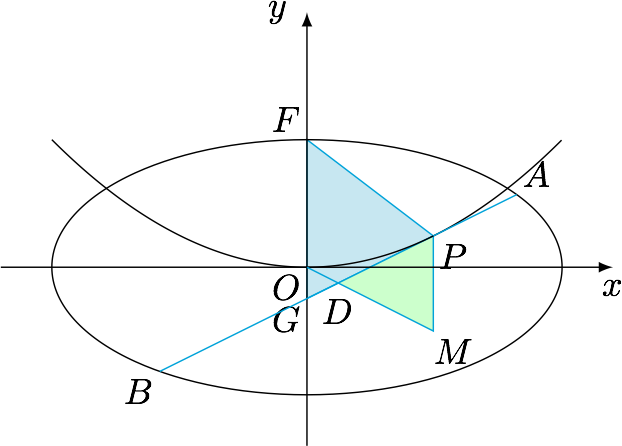
(2) 设$P$是$E$上的动点,且位于第一象限,$E$在点$P$处的切线$l$与$C$交于不同的两点$A,B$,线段$AB$的中点为$D$,直线$OD$与过$P$且垂直于$x$轴的直线交于点$M$.
(i) 求证:点$M$在定直线上;
(ii) 直线$l$与$y$轴交于点$G$,记$\triangle PFG$的面积为$S_1$,$\triangle PDM$的面积为$S_1$,求$\dfrac{S_1}{S_2}$的最大值及取得最大值时点$P$的坐标.
解 (1) 根据题意,有$F$点的坐标为$\left(0,\dfrac 12\right)$,于是$b=\dfrac 12$.又根据离心率为$\dfrac{\sqrt 3}2$可得$$a^2=4b^2=1,$$于是椭圆$C$的方程为$$x^2+4y^2=1.$$
(2) (i) 设$P(2t,2t^2)$,则切线$l$的方程为$$y=2tx-2t^2.$$由椭圆的“垂径定理”可得直线$OM$的斜率与直线$AB$的斜率满足$$k_{AB}\cdot k_{OM}=-\dfrac{b^2}{a^2},$$从而可得$k_{OM}=-\dfrac{1}{8t}$,于是不难计算得$M$的坐标为$\left(2t,-\dfrac 14\right)$,因此点$M$在定直线$y=-\dfrac 14$上.
(ii) 由$\triangle DPM$与$\triangle DGO$相似可得$$S_2=\dfrac{|PM|}{|PM|+|OG|}\cdot \dfrac 12\cdot |PM|\cdot d(O,PM),$$因此\[\begin{split} \dfrac{S_1}{S_2}&=\dfrac{ \left(2t^2+\dfrac 12\right)\cdot 2t}{2t\cdot\left(2t^2+\dfrac 14\right)\cdot\dfrac{2t^2+\dfrac 14}{4t^2+\dfrac 14}}\\ &=\dfrac{(8t^2+2)(16t^2+1)}{(8t^2+1)^2} \\ &\leqslant \left[\dfrac{(8t^2+2)+(16t^2+1)}2\right]^2\cdot \dfrac{1}{(8t^2+1)^2} \\ &=\dfrac 94,\end{split} \]等号当$$8t^2+2=16t^2+1$$时,即$t=\dfrac{1}{2\sqrt 2}$时取得.因此所求的最大值为$\dfrac 94$,此时点$P$的坐标为$\left(\dfrac{\sqrt 2}2,\dfrac 14\right)$.