正弦型波的合成

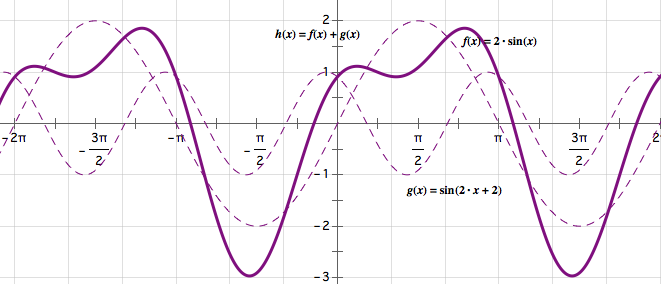
        我们都知道一般来说两个正弦型波合成后的波形会比较奇怪．

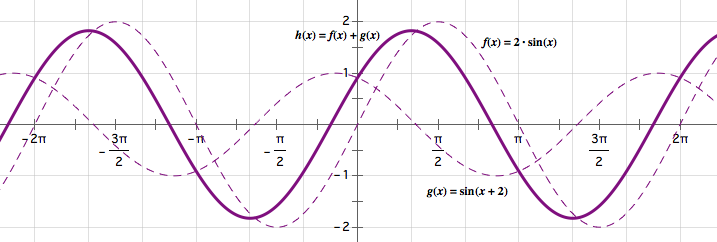
        但是同频率的正弦型波是可以合成为一个同样频率的正弦型波的，只不过合成的波的振幅和初相位会发生改变，如图．

         那么这种合成遵循什么样的规律呢？

---

 

考虑两个同频率波$f_1(x)=A_1\sin\left(\omega x+\varphi_1\right)$、$f_2(x)=A_2\sin\left(\omega x+\varphi_2\right)$的合成

$$f(x)=A\sin\left(\omega x+\varphi\right).$$

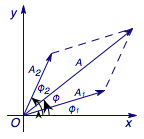
把$f_1(x)$、$f_2(x)$、$f(x)$分别看作向量

$$\begin{split}\vec a&=\left(A_1\cos\left(\omega x+\varphi_1\right),A_1\sin\left(\omega x+\varphi_1\right)\right),\\\vec b&=\left(A_2\cos\left(\omega x+\varphi_2\right),A_2\sin\left(\omega x+\varphi_2\right)\right),\\\vec c&=\vec a+\vec b,\end{split}$$ 的纵坐标，这样我们就可以将正弦型波的合成看作为向量的合成，如图．

因此，我们可以这样看待辅助角公式

$$a\sin x+b\cos x=a\sin x+b\sin\left(x+\dfrac{\pi}2\right)=\sqrt{a^2+b^2}\sin\left(x+\varphi\right),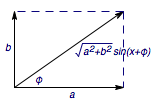$$ 类似的，我们也可以快速得到这样的结果： $$\sin x +\sin\left(x+\dfrac{\pi}3\right)=\sqrt 3\sin\left(x+\dfrac{\pi}6\right).$$

接下来我们可以自己命制一道练习题．

求函数$f(x)=2\sin\left(x+\dfrac{\pi}4\right)+3\sin\left(x+\dfrac{\pi}3\right)$的最大值．