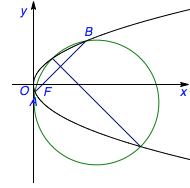
已知抛物线\(y^2=2px(p>0)\)，\(AB\)为过抛物线焦点\(F\)的弦，\(AB\)的中垂线交抛物线\(E\)于点\(M\)、\(N\)．若\(A\)、\(M\)、\(B\)、\(N\)四点共圆，求直线\(AB\)的方程．
e，作为数学常数，是自然对数函数的底数．有时称它为欧拉数（Euler number），以瑞士数学家欧拉命名；也有个较鲜见的名字纳皮尔常数，以纪念苏格兰数学家约翰·纳皮尔 (John Napier)引进对数．它就像圆周率π和虚数单位i，e是数学中最重要的常数之一．那么如何证明e是无理数呢？
圆周率用字母π（读作pài）表示，是一个常数（约等于3.141592654），是代表圆周长和直径的比值．它是一个无理数，即无限不循环小数．在日常生活中，通常都用3.14代表圆周率去进行近似计算．而用十位小数3.141592654便足以应付一般计算．即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百位．那么如何证明π是无理数呢？
1、设$\triangle ABC$的垂心为$H$，中点三角形的内切圆为$\Gamma$，圆心为$S$，直线$l\parallel AB$，直线$m\parallel AC$，且都与$\Gamma$相切（$AB$与$l$，$AC$与$m$分别在$S$的同侧），$l$与$m$交于$T$，射线$AT$上一点$N$满足$AN=2AT$，$Q$是优弧$BAC$的中点，四边形$AHRQ$为平行四边形，证明：$HR\perp RN$．
这是2014年北京市海淀区一模试题的压轴题：
在平面直角坐标系中，对于任意相邻三点都不共线的有序整点列（整点即横纵坐标都是整数的点），\(A(n):A_1,A_2,\cdots,A_n\)与\(B(n):B_1,B_2,\cdots,B_n\)，其中\(n\geqslant 3\)，若同时满足：
①点列的起点和终点分别相同；
②线段\(A_iA_{i+1}\perp B_iB_{i+1}\)，其中\(i=1,2,\cdots,n-1\)．则称\(A(n)\)与\(B(n)\)互为正交点列．
（1）求\(A(3):A_1(0,2),A_2(3,0),A_3(5,2)\)的正交点列；
（2）判断：\(A(4):A_1(0,0),A_2(3,1),A_3(6,0),A_4(9,1)\)是否存在正交点列\(B(4)\)，并说明理由．
（3）对于任意\(n\geqslant 5\)，\(n\in\mathcal N\)，是否都存在无正交点列的有序整点列\(A(n)\)？并证明你的结论．
这是2014年东城区一模压轴题： 已知集合\(\{1,2,3,4,\cdots,n\}(n\geqslant 3\)，若该集合具有下列性质的子集：每个子集至少含有\(2\)个元素，且每个子集中任意两个元素之差的绝对值大于\(1\)，则称这些子集为离散子集，记离散子集的个数为\(a_n\)．
（1）当\(n=5\)时，写出所有离散子集；
（2）求\(a_{10}\);
（3）记\[S_n=\frac {a_3}{2^3}+\frac {a_4}{2^4}+\cdots+\frac {a_n}{2^n},\]求证：\(S_n<2\)． 继续阅读
1、（2014年北京市海淀区高一期末试题）已知函数\(f(x)=\sin\dfrac{\pi}2x\)，任取\(t\in\mathcal R\)，记函数\(f(x)\)在区间\([t,t+1]\)上的最大值为\(M_t\)，最小值为\(m_t\)，记\(h(t)=M_t-m_t\)．则关于函数\(h(t)\)有如下结论：
① 函数\(h(t)\)为偶函数；
② 函数\(h(t)\)的值域为\(\left[1-\dfrac{\sqrt 2}2,1\right]\)；
③ 函数\(h(t)\)的周期为\(2\)；
④ 函数\(h(t)\)的单调增区间为\(\left[2k+\dfrac 12,2k+\dfrac 32\right],k\in \mathcal Z\)，
其中正确的结论有________．（填上所有正确的结论序号）
2、（2014年北京市海淀区高一期末考试题）已知函数\(f(x)\)的定义域为\([0,1]\)，且\(f(x)\)的图象连续不间断．若函数\(f(x)\)满足：对于给定的\(m\)（其中\(m\in\mathcal R\)且\(m\in(0,1)\)，存在\(x_0\in [0,1-m]\)，使得\(f(x_0)=f(x_0+m)\)，则称\(f(x)\)具有性质\(P(m)\)．
（1）已知函数\(f(x)=\left(x-\dfrac 12\right)^2,x\in [0,1]\)，判断\(f(x)\)是否具有性质\(P\left(\dfrac 13\right)\)，并说明理由；
（2）已知函数\[f(x)=\begin{cases}-4x+1,&0\leqslant x<\dfrac 14,\\4x-1,&\dfrac 14\leqslant x<\dfrac 34,\\-4x+5,&\dfrac 34\leqslant x\leqslant 1,\end{cases}\]若\(f(x)\)具有性质\(P(m)\)，求\(m\)的最大值；
（3）若函数\(f(x)\)的定义域为\([0,1]\)，且\(f(x)\)的图象连续不间断，又满足\(f(0)=f(1)\)，求证：对任意\(k\in\mathcal N^*\)且\(k\geqslant 2\)，函数\(f(x)\)具有性质\(P\left(\dfrac 1k\right)\)．
3、（2013年北京市西城区高一期末考试题）已知函数\(g(x)={\log_a}x\),其中\(a>1\)．
（1）当\(x\in[0,1]\)时，\(g(a^x+2)>1\)恒成立，求\(a\)的取值范围；
（2）设\(m(x)\)是定义在\([s,t]\)上的函数，在\((s,t)\)内任取\(n-1\)个数\(x_1,x_2,\cdots,x_{n-2},x_{n-1}\)，设\(x_1<x_2<\cdots<x_{n-2}<x_{n-1}\)，令\(s=x_0\)，\(t=x_n\)，如果存在一个常数\(M>0\)，使得\[\sum_{i=1}^n\left|m(x_i)-m(x_{i-1})\right|\leqslant M\]恒成立，则称函数\(m(x)\)在区间\([s,t]\)上具有性质\(P\)． 试判断函数\(f(x)=\left|g(x)\right|\)在区间\(\left[\dfrac 1a,a^2\right]\)上是否具有性质\(P\)？若具有性质\(P\)，请求出\(M\)的最小值；若不具有性质\(P\)，请说明理由．
