讨论某个含参方程的根的个数是高中数学函数模块中经常遇到的问题．这类题一般通过将方程的解看做是两个函数的图象交点的横坐标来解决，其本质为将一维的方程的根的问题升到二维的函数图象的交点问题．这就好比是如果想搞清楚某个城市的道路情况，从空中鸟瞰往往比遍历一遍这个城市效率高得多．接下来，我们一起欣赏一道小题．
讨论关于\(x\)的方程\[\left(x^2-1\right)^2-2\left|x^2-1\right|+k=0\]的根的个数．
这次是2008年英国数学奥林匹克的一道试题（2008/9 British Mathematical Olympiad,Round 2）：
求所有的函数\(f:\mathcal R\to \mathcal R\)，使得对任意\(x,y\in\mathcal R\)有
\[f(x^3)+f(y^3)=(x+y)\left[f(x^2)+f(y^2)-f(xy)\right].\]
题目来自百度贴吧．
已知整系数二次方程\(ax^2+bx+c=0\)的两个不同实根均在区间\((1,2)\)上，求正整数\(a\)的最小值．
我很快就构造了\(a=5\)的情形：
根据题目要求，有\[\begin{cases}a+b+c>0\\4a+2b+c>0\\-\frac{b}{2a}\in (1,2)\\b^2-4ac>0\end{cases}\]
设想一个差不多的方程\[ax^2-3ax+2a=0,\]此时\[a=a,b=-3a,c=2a.\]但该方程的\(b\)或者\(c\)需要增大一点，使得\[a+b+c>0\land 4a+2b+c>0.\]但这样会使得判别式失控，我们需要单独处理．
（1）若令\(a=a+1\)，则有\[(-3a)^2-4\cdot (a+1)\cdot 2a=a^2-8a>0.\]
（2）若令\(b=-3a+1\)，则有\[(-3a+1)^2-4\cdot a\cdot 2a=a^2-6a+1>0.\]
（3）若令\(c=2a+1\)，则有\[(-3a)^2-4\cdot a\cdot (2a+1)=a^2-4a>0.\]
看起来方案（3）最科学，于是\(a\)可以取\(5\)，此时\(b=-15,c=11\)，验证通过！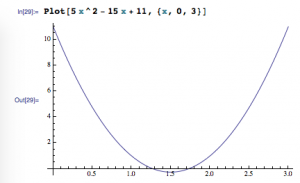
这样我们构造了\(a=5\)的情形．
接下来需要说明\(a=1,2,3,4\)不可能，我是用对称轴和判别式很繁琐的完成这个任务的，大家有更好的方法吗？
2015年3月6日更新扒拉题的解法，http://tieba.baidu.com/p/3575904855．
由题意所得的不等式组可以整理为\[\begin{cases}c>-b-a\\c>-2b-4a\\-4a<b<-2a\\c<\frac{1}{4a}\cdot b^2\end{cases}\]其中将\(a\)看作参数，在坐标系\(bOc\)中画出可行域
情形1：当\(-3a\leqslant b<-2a\)时，设\(b=-2a-n\)，其中\(0<n\leqslant a\)，\(n\in\mathcal Z\)．此时\[-b-a<c<\dfrac{b^2}{4a},\]要使该范围内存在整数\(c\)，需\[\dfrac{b^2}{4a}-(-b-a)>1\]将\(b=-2a-n\)代入整理得\[n^2>4a,\]要使得在可\(0<n\leqslant a\)范围内存在整数\(n\)，只需\[a^2>4a\]解得\[a>4.\]
情形2：当\(-4a<b<-3a\)时，设\(b=-4a-n\)，其中\(0<n<a\)，\(n\in\mathcal Z\)．此时\[-2b-4a<c<\dfrac{b^2}{4a},\]要使该范围内存在整数\(c\)，需\[\dfrac{b^2}{4a}-(-2b-4a)>1\]将\(b=-4a-n\)代入整理得\[n^2>4a,\]要使得在\(0<n<a\)范围内存在\(n\)，只需\[(a-1)^2>4a,\]解得\[0<a<3-2\sqrt 2\lor a>3+2\sqrt 2.\]
综合情形1与情形2可知，\(a\geqslant 5\)，进而可以利用情形1构造\(a=5\)的例子，从略．
2015年8月6日更新解法，来源于帷幕讨论组的zhj．
记\(f(x)=ax^2+bx+c\)，并设两根分别为\(x_1\)和\(x_2\)，则\[f(1)\geqslant 1\land f(2)\geqslant 1,\]于是\[\begin{split}f(1)\cdot f(2)&=a\left(1-x_1\right)\left(1-x_2\right)\cdot a\left(2-x_1\right)\left(2-x_2\right)\\&\leqslant a^2\cdot\left[\dfrac{\left(x_1-1\right)+\left(x_2-1\right)+\left(2-x_1\right)+\left(2-x_2\right)}4\right]^4&=\dfrac{a^2}{16},\end{split}\]等号取得的条件为\(x_1=x_2=\dfrac 32\)，因此可得\(a>4\)．
令\(f(1)=f(2)=1\)，\(a=5\)即得解得\(f(x)=5x^2-15x+11\)，于是\(a\)的最小解为\(5\)．
今天换换口味吧，来一道清爽可口的概率题．对计数有感的同学们可以试试啦！
已知袋中有\(10\)个小球，其中有\(5\)个红球，\(3\)个黄球，\(2\)个绿球．每次从袋中不放回的取出一个球，问红球首先被全部取出的概率．
今天继续昨天的话题——代数条件的直观化，带来的题目是一道来自北京市海淀区高三的函数小题．
已知函数\(f(x)=\dfrac{\sin x}{x}\)，则满足\[f\left(\frac{n\pi}{6}\right)<f\left(\frac{n\pi}{6}+\frac{\pi}6\right)\]的正整数\(n\)的最小值为________．
裂项求和是数列求和的一种重要方法．但由于对等差数列求和的倒序相加法和对等比数列（差比数列）的错位相减法的深（根）入（深）人（蒂）心（固），我几乎都忽略了裂项求和也可以应用于这些基本数列的求和．
例1．求和：\[2+5+8+\cdots+3n-1.\] 对通项进行裂项：\[3n-1=(an^2+bn)-\left[a(n-1)^2+b(n-1)\right]=2an-a+b,\]其中\(a,b\)为待定系数． 易得\[a=\frac 32,b=\frac 12.\] 于是\[2+5+8+\cdots+3n-1=\frac 32n^2+\frac 12n.\]
例2．求和：\[3+3^2+3^3+\cdots+3^n.\] 对通项进行裂项\[3^n=a\cdot 3^n-a\cdot 3^{n-1}=\frac{2a}3\cdot 3^n,\]其中\(a\)为待定系数． 易得\[a=\frac 32.\] 于是\[3+3^2+3^3+\cdots+3^n=\frac 32\cdot 3^n-\frac 32.\]
例3．求和\[1\cdot 2+3\cdot 2^2+5\cdot 2^3+\cdots+(2n-1)\cdot 2^n.\] 对通项进行裂项\[\begin{split}(2n-1)\cdot 2^n&=(an+b)\cdot 2^n-\left[a(n-1)+b\right]\cdot 2^{n-1}\\&=\left(\frac a2\cdot n+\frac{a}2+\frac{b}2\right)\cdot 2^n,\end{split}\]其中\(a,b\)为待定系数． 易得\[a=4,b=-6.\] 于是\[1\cdot 2+3\cdot 2^2+5\cdot 2^3+\cdots+(2n-1)\cdot 2^n=(4n-6)\cdot 2^n+6.\]
例4．求和\[1\cdot 2+2^2\cdot 2^2+3^2\cdot 2^3+\cdots+n^2\cdot 2^n.\] 对通项进行裂项\[\begin{split}n^2\cdot 2^n&=(an^2+bn+c)\cdot 2^n-\left[a(n-1)^2+b(n-1)+c\right]\cdot 2^{n-1}\\&=\left[\frac a2\cdot n^2+\left(a+\frac b2\right)n-\frac a2+\frac b2+\frac c2\right]\cdot 2^n,\end{split}\]其中\(a,b,c\)为待定系数． 易得\[a=2,b=-4,c=6.\] 于是\[1\cdot 2+2^2\cdot 2^2+3^2\cdot 2^3+\cdots+n^2\cdot 2^n=(2n^2-4n+6)\cdot 2^n-6.\]
综上所述，用待定系数裂项法求差比数列（甚至是高阶差比数列）的前$n$项和非常简便，尤其是算完待定系数之后无需整理，可谓居家旅行杀人越货之利器也．
这次我们来看看2010年北京高考理科数学解析几何试题中的条件转化．
在平面直角坐标系\(xOy\)中，点\(B\)与\(A(-1,1)\)关于原点对称，\(P\)是动点，且直线\(AP\)与\(BP\)的斜率之积等于\(-\dfrac 13\)．
（1）求动点\(P\)的轨迹方程；
（2）设直线\(AP\)和\(BP\)分别与直线\(x=3\)交于点\(M\)，\(N\)，问：是否存在点\(P\)使得\(\triangle PAB\)与\(\triangle PMN\)的面积相等？若存在，求出点\(P\)的坐标；若不存在，请说明理由．
今天继续带来一道代数条件直观化的试题．原题是2015年北京市海淀区高三期末文科压轴题．
已知数列\(\{a_n\}\)是公差为\(d\)，首项\(a_1=1\)的等差数列，问是否存在实数\(d\)使得数列\(\left\{\dfrac{1}{a_n}\right\}\)满足：可以从中取出无限多项，并按原来的先后次序排成一个等差数列？若存在，求出所有满足条件的\(d\)的值；若不存在，说明理由．
这是2013年全国新课标I卷理科数学的选择题最后一题（第12题），主要考察变化中的规律探索．同时，本题也是代数条件直观化的一道好题．数形结合思想最强大、最优美的一面就是：对繁杂晦涩的代数算式运用几何直观的方式将蕴含的本质挖掘出来，从而使得问题获得极大简化．
设三角形\(A_nB_nC_n\)的三边长分别为\(a_n,b_n,c_n\)，三角形\(A_nB_nC_n\)的面积为\(S_n\)，\(n=1,2,3,\cdots\)，若\(b_1>c_1\)，\(b_1+c_1=2a_1\)，且满足\[\begin{split}a_{n+1}&=a_n,\\b_{n+1}&=\frac{c_n+a_n}2,\\c_{n+1}&=\frac{b_n+a_n}2,\end{split}\]则（ ）
A．\(\{S_n\}\)为递减数列
B．\(\{S_n\}\)为递增数列
C．\(\{S_{2n-1}\}\)为递增数列，\(\{S_{2n}\}\)为递减数列
D．\(\{S_{2n-1}\}\)为递减数列，\(\{S_{2n}\}\)为递增数列
