已知\(MN\)是过椭圆\(\dfrac{x^2}9+\dfrac{y^2}5=1\)的左焦点\(F\)的直线（\(M,N\)在椭圆上），\(A(1,0)\)是椭圆长轴上的一个定点．直线\(MA\)，\(NA\)分别交椭圆于\(P\)、\(Q\)，求证：直线\(PQ\)与直线\(MN\)的斜率之比为定值．
已知\(F\)为椭圆\(\dfrac{x^2}5+y^2=1\)的右焦点，第一象限内的点\(M\)在椭圆上，若\(MF\)与\(x\)轴垂直，直线\(MN\)与圆\(x^2+y^2=1\)相切于第四象限内的点\(N\)，则\(NF\)的长度为_______．
已知数列\(a,b,c\)成等比数列，\(a,\dfrac{b(b-1)}{2},c\)为等差数列，当\(1<a<3<c<7\)时，\(b\)的取值范围是_______．
在平面直角坐标系\(xOy\)中，已知圆\(O_1\)，圆\(O_2\)均与\(x\)轴相切，且圆心\(O_1,O_2\)与原点\(O\)共线，\(O_1,O_2\)两点的横坐标之积为\(5\)．设圆\(O_1\)与圆\(O_2\)相交于\(P\)、\(Q\)两点，直线\(l:2x-y-8=0\)，则\(P\)到直线\(l\)的距离的最小值为_______．
已知三角形\(ABC\)中，\(\overrightarrow{CP}=\dfrac 12\left(\overrightarrow{CA}+\overrightarrow{CB}\right)\)，\(\left|\overrightarrow{CP}\right|=\dfrac 12\left|\overrightarrow{AB}\right|=1\)．点\(Q\)是线段\(AB\)上一点，且\(\overrightarrow{CQ}\cdot\overrightarrow{CP}=\dfrac 12\)，则\(\left|\overrightarrow{CQ}\right|\)的取值范围是_______．
求函数\[f(x)=\cos x+\sqrt{\cos^2x-4\sqrt{2}\cos x+4\sin x+9}\]的最大值与最小值．
1、已知\(z_1,z_2\in\mathcal C^*\)，\(\left|z_1+z_2\right|=\left|z_1-z_2\right|\)．求证：\(\dfrac{z_1^2}{z_2^2}<0\)．
2、设\(n\in\mathcal N^* \),试判断是否存在\(a\in\mathcal R\)，使\[\sqrt{2n+1}\cdot\prod_{k=1}^{n}{\left(1-\dfrac{1}{2k}\right)}<a\]恒成立？请说明理由．
3、已知\(m,n\in\mathcal R\)，求证：\[{\rm e}^\frac{m+n}2<\dfrac{{\rm e}^m-{\rm e}^n}{m-n}<\dfrac{{\rm e}^m+{\rm e}^n}2.\]
4、已知数列\(\left\{a_n\right\}\)的通项公式为\[a_n=\dfrac{3\cdot 2^n}{4\cdot 4^n-6\cdot 2^n+2},\]求证：\(\sum\limits_{k=1}^na_k<\dfrac 32\)．
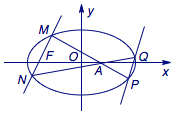
5、已知离心率为\(\dfrac{\sqrt 3}2\)的椭圆\(C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)（\(a>b>0\)）与直线\(x=2\)相交于\(P\)、\(Q\)两点（点\(P\)在\(x\)轴上方），且\(PQ=2\)．点\(A\)、\(B\)是椭圆上位于直线\(PQ\)两侧的两个动点，且\(\angle APQ=\angle BPQ\)．
（1）求椭圆\(C\)的标准方程；
（2）求四边形\(APBQ\)面积的取值范围．
6、已知函数\(f(x)=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\)，\(x_1,x_2,x_3\in\mathcal R\)，且\(x_1<x_2<x_3\)．
（1）当\(x_1=0\)，\(x_2=1\)，\(x_3=2\)时，若方程\(f(x)=mx\)恰存在两个相等的实根，求实数\(m\)的值；
（2）求证：方程\(f'(x)=0\)有两个不相等的实数根；
（3）若方程\(f'(x)=0\)的两个实数根是\(\alpha\)，\(\beta\)（\(\alpha<\beta\)），试比较\(\dfrac{x_1+x_2}2\)与\(\alpha\)，\(\beta\)的大小关系，并说明理由．
7、已知函数\(f(x)=\ln{\left(\dfrac 12+\dfrac 12ax\right)}+x^2-ax\)（\(a\)为常数，且\(a>0\)）．
（1）若\(x=\dfrac 12\)是函数\(f(x)\)的一个极值点，求\(a\)的值；
（2）求证：当\(0<a\leqslant 2\)时，\(f(x)\)在\(\left[\dfrac 12,+\infty\right)\)上是增函数；
（3）若对任意的\(a\in (1,2)\)，总存在\(x_0\in\left[\dfrac 12,1\right]\)，使不等式\(f(x_0)>m\left(1-a^2\right)\)成立，求实数\(m\)的取值范围．
如图，过椭圆外一点引椭圆的两条切线\(PA\)与\(PB\)．椭圆上一点\(C\)处的切线与\(PA\)、\(PB\)分别交于\(M\)、\(N\)，即椭圆与三角形\(PMN\)旁切．求证：\(MN\)对椭圆的焦点\(F\)的张角大小与\(C\)点的位置无关．
已知圆\(x^2+y^2-6y+m=0\)和直线\(x+2y-3=0\)交于\(P\)、\(Q\)两点，且以\(PQ\)为直径的圆过原点，求\(m\)的值．
1、对于任意两个实数\(a,b\)，定义运算“\(*\)”如下：\[a*b=\begin{cases}a,a\leqslant b,\\b,a>b.\end{cases}\]那么函数\[f(x)=x^2*\left[(6-x)*(2x+15)\right]\]的最大值为_______．
2、已知\(x,y>0\)，且\(x+y=12\)，则\(\sqrt{x^2+1}+\sqrt{y^2+16}\)的最小值为_______．
3、已知向量序列：\(\overrightarrow{a_1},\overrightarrow{a_2},\cdots,\overrightarrow{a_n},\cdots\)满足如下条件：\(\left|\overrightarrow{a_1}\right|=4\left|\overrightarrow{d}\right|=2\)，\(2\overrightarrow{a_1}\cdot\overrightarrow{d}=-1\)且\(\overrightarrow{a_n}-\overrightarrow{a_{n-1}}=\overrightarrow{d}\)（\(n=2,3,4,\cdots\)）．若\(\overrightarrow{a_1}\cdot\overrightarrow{a_k}=0\)，则\(k=\)_______；\(\left|\overrightarrow{a_i}\right|\)（\(i=1,2,3,\cdots\)）中最小项对应的\(i=\)_______．
4、如图，从\(A\)到\(B\)，每次只能向右或者向上移动一步，有_______种不同的走法．
5、已知实数\(a>0\)，\(f(x)=\begin{cases}x^2-2ax,&x\leqslant 1,\\{\log_{\frac 12}}x,&x>1.\end{cases}\)若方程\(f(x)=-\dfrac 34a^2\)有且仅有两个不等实根，且较大实根大于\(2\)，则实数\(a\)的取值范围是_______．
