已知双曲线 $\Gamma:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$（$a,b>0$），$F$ 是双曲线的右焦点，$e$ 为双曲线的离心率．
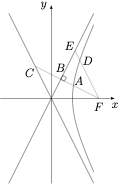
1、过 $F$ 作渐近线的垂线，与双曲线和两条渐近线依次交于 $A,B,C$．
① 若 $\overrightarrow{FA}=\lambda\overrightarrow{FB}$，求 $e$；
② 若 $\overrightarrow{FB}=\mu\overrightarrow{FC}$，求 $e$．
2、若 $F$ 作渐近线的平行线，与双曲线以及双曲线的另一条渐近线交于 $D,E$，若 $\overrightarrow{FD}=t\overrightarrow{FE}$，求 $e$．
已知椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 上三点 $P,A,B$，其中 $P(x_0,y_0)$，若直线 $PA,PB$ 的斜率分别为 $k_1,k_2$，求直线 $AB$ 的方程．
已知椭圆 $E: \dfrac{x^2}{4}+y^2=1$ 和 $A(-1,0), B\left(\dfrac{3}{5}, \dfrac{4}{5}\right)$，$ P$ 是直线 $y=2$ 上的动点，$C$ 是线段 $P A$ 与椭圆 $E$ 的交点，线段 $P B$ 的延长线与椭圆 $E$ 交于点 $D$．求证：直线 $C D$ 过定点．
已知点 $B(-2,-1)$ 是椭圆 $E:\dfrac{x^2}{16}+\dfrac{y^2}{12}=1$ 内一点，过点 $A(-8,0)$ 作直线 $l$ 与椭圆交于 $P, Q$ 两点，直线 $P B$ 与椭圆交于另一点 $N$，证明：直线 $Q N$ 过定点．
已知 $\triangle PAB,\triangle PCD$ 均为正三角形且 $PA=2PC$，则 $\dfrac{BD}{AC}$ 的取值范围是_____．
已知 $x,y\in (0,1)$，求证：\[\left|x\sin\dfrac{1}{x^2}-y\sin\dfrac{1}{y^2}\right|\leqslant 3\sqrt[3]{|x-y|}.\]
已知 $\triangle ABC$ 中，$AB=5$，$BC=12$，$CA=13$，$P$ 是 $\triangle ABC$ 内一点且 $\angle APB=\angle BPC=\angle CPA=120^\circ$，则 $\overrightarrow{PA}\cdot \overrightarrow{PB}+\overrightarrow{PB}\cdot \overrightarrow{PC}+\overrightarrow{PC}\cdot \overrightarrow{PA}=$ _____．
2025年广东深圳宝安区一模数学试卷 #11
已知函数 $f(x)$ 为 $\mathbb R$ 上的奇函数，当 $0\leqslant x\leqslant 2$ 时，$f(x)=x^3-3 x$，且 $f(x)$ 的图象关于点 $(2,2)$ 中心对称，则下列说法正确的是（ ）
A．$f(3)=6$
B．函数 $y=f(x)-5$ 有三个零点
C．$g(x)=f(x)-x$ 是周期为 $4$ 的周期函数
D．线段 $y=x+\dfrac{16\sqrt 3}9,x\in[-2,10]$ 与 $y=f(x),x\in[-2,10]$ 的图象有 $6$ 个交点
2025年广东深圳宝安区一模数学试卷 #14
记锐角 $\triangle ABC$ 的内角 $A,B,C$ 的对边分别为 $a,b,c$，已知 $\dfrac{\sin (A-B)}{\cos B}=\dfrac{\sin (A-C)}{\cos C}$，且 $a\sin C=1$，则 $\dfrac 1{a^2}+\dfrac 1{b^2}$ 的最大值为 _____．
2025年广东深圳宝安区一模数学试卷 #18
在平面直角坐标系中 $x Oy$，椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的离心率为 $\dfrac{\sqrt 3}2$，点 $\left(-\sqrt 3,\dfrac 1 2\right)$ 在椭圆 $C$ 上．
1、求椭圆 $C$ 的方程；
2、设椭圆 $C$ 的左、右顶点分别为 $A,B$，点 $P,Q$ 为椭圆上异于 $A,B$ 的两动点，记直线 $AP$ 的斜率为 $k_1$，直线 $QB$ 的斜率为 $k_2$，已知 $k_1=7 k_2$．
① 求证：直线 $PQ$ 恒过 $x$ 轴上一定点；
② 设 $\triangle PQB$ 和 $\triangle PQA$ 的面积分别为 $S_1,S_2$，求 $\left|S_1-S_2\right|$ 的最大值．
