Math173

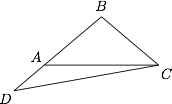
在$\triangle ABC$内取一点$O$，设$\overrightarrow e_1,\overrightarrow e_2,\overrightarrow e_3$分别是$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$上的单位向量，求$m=\left|\overrightarrow e_1+\overrightarrow e_2+\overrightarrow e_3\right|$的取值范围．

继续阅读 →

已知数列$\{a_n\}$满足$a_1=1$，$a_{n+1}\cdot a_n=\dfrac 1n$($n\in\mathbb N^*$)．
(1) 求证：$\dfrac{a_{n+2}}{n}=\dfrac{a_n}{n+1}$；
(2) 求证：$2\left(\sqrt{n+1}-1\right)\leqslant \dfrac{1}{2a_3}+\dfrac{1}{3a_4}+\cdots+\dfrac{1}{(n+1)a_{n+2}}\leqslant n$．

继续阅读 →

平面上有两条线段$AB=3$，$AC=5$，且$\angle BAC=\dfrac{\pi}6$，则线段$AB$和$AC$在该平面上任意一条直线$l$上的投影的长度之和的取值范围是_________．
继续阅读 →

如图，$\triangle ABC$中，$BA=BC$，延长$BA$至点$D$使$BD=AC$，若$\angle BCD=50^\circ$，求证：$\angle B=100^\circ$．

继续阅读 →

函数$f(x)=\dfrac{4x}{x+1}$($x>0$)，$g(x)=\dfrac 12\left(|x-a|-|x-b|\right)$($a<b$)，若对$\forall x_1>0$，$\exists x_2\leqslant x_1$，$g(x_2)=f(x_1)$，则$2a+b$的最大值为________．

继续阅读 →

若$\triangle ABC$沿三条中位线折起后能够拼接成一个三棱锥，则称这样的$\triangle ABC$为和谐三角形．设$\triangle ABC$的三个内角分别为$A,B,C$，则下列条件中能够确定为和谐三角形的有________．
① $A:B:C=7:20:25$；
② $\sin A:\sin B:\sin C=7:20:25$；
③ $\cos A:\cos B:\cos C=7:20:25$；
④ $\tan A:\tan B:\tan C=7:20:25$．

继续阅读 →

一张长方形白纸$ABCD$，其中$AD=1$，$AB=a$($a\geqslant 1$)．设$D_1$是边$AB$上一点，记$AD_1=x$．现拿起白纸的顶点$D$，将点$D$折向$D_1$，并保证端点$D$与$D_1$重合．设折后得到的图形中，不在原来的长方形$ABCD$范围的部分面积为$S$．
(1) 用$a$和$x$表示$S$；
(2) 当$a=1$时，在$D_1$点从$A$移动到$B$的过程中，求$S$的最大值．
继续阅读 →

已知函数$g(x)={\log_2}x,x\in(0,2)$，若关于$x$的方程$|g(x)|^2+m|g(x)|+2m+3=0$有三个不同的实数解，则实数$m$的取值范围是_______．

继续阅读 →