Math173

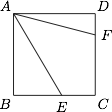
已知正方形 $ABCD$ 的边长为 $1$，点 $E,F$ 分别在边 $BC$ 与 $CD$ 上（包含端点），且 $\angle EAF=45^\circ$，则 $\sqrt{BE^2+DF^2}$ 的取值范围是 ______．

继续阅读 →

在三棱锥 $D-ABC$ 中，已知 $AB=2$，$\overrightarrow{AC}\cdot\overrightarrow{BD}=-3$．设 $AD=a$，$BC=b$，$CD=c$，则 $\dfrac{c^2}{ab+1}$ 的最小值为______．

继续阅读 →

定义在正整数集且在正整数集上取值的函数 $f(x)$ 满足 $f(1)\neq1$，且对 $\forall n\in\mathbb{N}^{\ast}$，有 $f\left(n\right)+f\left(n+1\right)$ $+f(f(n))=3n+1$，则 $f(2015)=$_______．

继续阅读 →

若定义在 $\mathbb R$ 上的函数 $f(x)=\left|{\sin x+\dfrac{2}{3+\sin x}+t}\right|$ 最大值记为 $g(t)$，则函数 $g(t)$ 的最小值为______．

继续阅读 →

已知 $a,b,c$ 为正整数，函数 $f(x)=ax+\dfrac cx$，关于 $x$ 的方程 $f(x)=b$ 在 $(0,1)$ 上有两个实数解，若这样的 $b$ 有且只有 $2$ 个，那么 $a+c$ 的最小值为_______．

继续阅读 →

已知实数 $x,y,z$ 满足 $x^2+2y^2+3z^2=4,$ 若 $T=xy+yz,$ 则 $T$ 的取值范围是（　　）
A．$\left[-\dfrac{\sqrt6}3,\dfrac{\sqrt6}3\right]$
B．$\left[-\dfrac{\sqrt6}6,\dfrac{2\sqrt6}3\right]$
C．$\left[-\dfrac{\sqrt6}3,\dfrac{\sqrt3}3\right]$
D．$\left[-\dfrac{2\sqrt6}3,\dfrac{2\sqrt6}3\right]$

继续阅读 →

函数 $f(x)=-x^2+3x+a$，$g(x)=2^x-x^2$，若 $f(g(x))\geqslant 0$ 对于 $x\in[0,1]$ 恒成立，则实数 $a$ 的取值范围是（　　）

A．$[-\mathrm{e},+\infty)$
B．$[-\ln 2,+\infty)$
C．$[-2,+\infty)$
D．$\left(-\dfrac12,0\right]$

继续阅读 →

已知 $x_1,x_2$ 是关于 $x$ 的方程 $ax^2+bx+c=0$ 的两根，且 $1<x_1<x_2<2$，$a,b,c\in \mathbb Z$．则当正整数 $a$ 取得最小值时，$b+c$ 的值为 （　　）
A．$-5$
B．$-4$
C．$-1$
D．$3$

继续阅读 →

求使得 $\sqrt{k^2-2004k}$ 是正整数的正整数 $k$ 的个数．

继续阅读 →

已知变量 $x$ 和 $\theta$ 都在 $\mathbb R$ 上变化，则 $\dfrac{x^2+2x\sin\theta+2}{x^2+2x\cos\theta+2}$ 的取值范围是_______．

继续阅读 →