2026年1月湖南雅礼中学高三期末数学考试 #11
已知 $g(x)=2+m\cos x+n\sin x+M\cos 2 x+N\sin 2 x$,其中 $m,n,M,N$ 为常数, 且 $g(x)\geqslant 0$ 对任意 $x\in\mathbb R$ 恒成立,则( )
A.$m^2+n^2\leqslant 8$
B.$M^2+N^2>4$
C.$|m|+|n|+|M|+|N|\leqslant 2\sqrt 2+4$
D.$g(x)\leqslant 6$
2026年1月湖南雅礼中学高三期末数学考试 #11
已知 $g(x)=2+m\cos x+n\sin x+M\cos 2 x+N\sin 2 x$,其中 $m,n,M,N$ 为常数, 且 $g(x)\geqslant 0$ 对任意 $x\in\mathbb R$ 恒成立,则( )
A.$m^2+n^2\leqslant 8$
B.$M^2+N^2>4$
C.$|m|+|n|+|M|+|N|\leqslant 2\sqrt 2+4$
D.$g(x)\leqslant 6$
2026年1月湖南雅礼中学高三期末数学考试 #8
已知 $\triangle ABC$ 是锐角三角形,$CA>CB>AB=1$,且 $BC\cdot\sin B=2$,则 $\triangle ABC$ 的内接正方形的面积最大值为( )
A.$\dfrac 4 9$
B.$1$
C.$\dfrac 9{16}$
D.$4$
2012年高考四川卷 #12
设函数 $f(x)=2x-\cos x$,$\{a_{n}\}$ 是公差为 $\dfrac{\pi}{8}$ 的等差数列,\[f(a_{1})+f(a_{2})+\cdots+f(a_{5})=5\pi,\]则 $f^2(a_{3})-a_{1}a_{5}=$ ( )
A.$0$
B.$\dfrac{1}{16}\pi^{2}$
C.$\dfrac{1}{8}\pi^{2}$
D.$\dfrac{13}{16}\pi^{2}$
己知椭圆 $E: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)经过点 $A(2,3)$,$F_1, F_2$ 分别为 $E$ 的左、右焦点,率心率 $e=\dfrac{1}{2}$.
1、求椭圆 $E$ 的方程;
2、求 $\angle F_1 A F_2$ 的角平分线所在直线 $l$ 的方程;
3、过点 $F_2$ 且斜率为 $k_1$ 的直线 $l_1$ 交椭圆 $E$ 于 $M, N$ 两点,记直线 $A M, A N$ 的斜率分别为 $k_2, k_3$,是否存在常数 $\lambda$,使得 $k_2+k_3-\lambda k_1$ 为定值?若存在,求出 $\lambda$ 及该定值;若不存在,请说明理由.
已知椭圆 $E: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)左、右顶点与上顶点分别为 $A, B, C$,离心率 $e$ 为 $\dfrac{\sqrt{3}}{2}$,$ \triangle A B C$ 的面积为 $2$.
1、求椭圆 $E$ 的标准方程;
2、点 $D$ 为第一象限 $E$ 上不同于顶点的动点,直线 $B D$ 与直线 $A C$ 交于点 $M$,直线 $C D$ 与 $x$ 轴交于点 $N$.证明:直线 $M N$ 过定点.
已知实数 $x,y$ 满足 $\left(\sqrt{x^2+1}-x\right)\left(\sqrt{y^2+4}-y\right)=2$,则 $4^x+2^{y-1}$ 的最小值为_____.
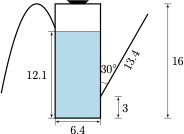
小申家里添置了一只新油壶,如图所示.该油壶的瓶身是一个底面直径为 $6.4~{\rm cm}$,高 $16~{\rm cm}$ 的圆柱体(不计厚度),瓶内装有 $12.1~{\rm cm}$ 高的油.其壶嘴长度为 $13.4~{\rm cm}$(不计体积),且壶嘴与瓶身的夹角为 $30^{\circ}$,壶嘴的底部距离底面的高度为 $3~{\rm cm}$.现将油壶从壶底一端缓慢倾斜,当油刚好从壶嘴流出时,油壶的最小倾斜角度为_______(精确到 $0.01^{\circ}$).
2026年上海春季高考第20题(解析几何大题):
已知双曲线 $\Gamma:\dfrac{x^2}2-\dfrac{y^2}2=1$,过点 $M(m,0)$ 的直线 $l$ 与 $\Gamma$ 交于 $A, B$ 两点.
1、求双曲线 $\Gamma$ 的离心率;
2、若 $A(\sqrt 3,1)$,且 $B$ 是线段 $AM$ 的中点,$A,B$ 均在双曲线右支上,求直线 $l$ 的斜率;
3、设 $m>0$,双曲线 $\Gamma$ 的左、右焦点分别为 $F_1 , F_2$,点 $A$ 关于 $y$ 轴的对称点为 $A^{\prime}$.若 $\overrightarrow{F_1 A^{\prime}}\cdot\overrightarrow{F_2 B}=0$,求实数 $m$ 的取值范围.
已知数列 $a_1, a_2, \cdots, a_n$ 为严格单调递增的正整数数列,$\left\{a_1, a_2, \cdots, a_n\right\}$ 的子集有 $2^n$ 个,分别计算每个子集的元素和得到 $S_1, S_2, \cdots, S_{2^n}$(规定空集元素和为 $0$),已知 $S_1<S_2<\cdots<S_{2^n}$.
1、求 $S_{2^n}$ 的最小值.
2、求 $S_1, S_2, \cdots, S_{2^n}$ 方差的最小值.
3、求证:$a_1^2+a_2^2+\cdots+a_n^2 \geqslant \dfrac{4^n-1}{3}$.
已知函数 $f(x)=\ln ^2 x+a x^2+b x, x>0$.
1、当 $a=0$,$b=2 \mathrm{e}$ 时,证明:$f(x) \geqslant 3$;
2、若存在 $a\in\mathbb R$,使得函数 $f(x)$ 有 $3$ 个不同的极值点 $r, s, t$($r<s<t$).
① 求实数 $b$ 的取值范围;
② 证明:$f(s)>-\dfrac{5}{4}$.