已知 $f(x)=\dfrac{1}{x-a}+\dfrac{1}{x-b}$（$a, b \in \mathbb{R}$）．
1、若 $a=b=1$，解不等式 $f(x)>1$．
2、定义区间 $(m, n),[m, n),(m, n],[m, n]$ 的长度为 $n-m$，若 $a<b$，求 $f(x)>1$ 解集的区间长度或解集的区间长度之和（解集为几个区间的并集时）．
$\sin ^{2} 10^{\circ}+\cos ^{2} 40^{\circ}+\sin 10^{\circ} \cos 40^{\circ}=$ ________.
已知 $f(x)=\dfrac{\mathrm{e}^{x-1}}{x}-a x+a \ln x$，其中 $a \in \mathbb{R}$．
1、当 $a=\dfrac{1}{\mathrm{e}}$ 时，求 $f(x)$ 的单调区间．
2、当 $x>0$ 时，$f(x) \geqslant 0$，求 $a$ 的取值范围．
如图，在棱长为 $1$ 的正方体 $A B C D-A_{1} B_{1} C_{1} D_{1}$ 中，动点 $P$ 在线段 $A_{1} B$ 上，设 $l$ 是平面 $D D_{1} P$ 与平面 $C C_{1} P$ 的交线．
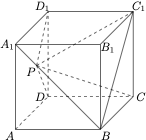
1、求证：$l\parallel C C_{1}$．
2、若 $P$ 是线段 $A_{1} B$ 上靠近 $A_{1}$ 的四等分点，求平面 $D D_{1} P$ 与平面 $C C_{1} P$ 所成二面角的正弦值．
一块三棱锥形状的余料 $P-A B C$，其三条侧棱 $P A, P B, P C$ 两两垂直．现需将其切割成直三棱柱，使得直三棱柱的侧棱与原三棱锥的一条侧棱平行或重合，若 $P A=a$，$P B=b$，$P C=c$，则切割得到的直三棱柱的最大体积为_______．（结果用 $a, b, c$ 表示，其中 $a, b, c$ 为正实数）
$(1-2 y)^{5}\left(2+\dfrac{1}{y}\right)^{4}$ 的展开式中 $y^{4}$ 的系数为（ ）
A．$-256$
B．$256$
C．$-1024$
D．$1024$
已知函数 $f(x)=x \mathrm{e}^{x}-\ln x-1$．
1、求证：函数 $f(x)$ 存在极小值点 $x_{0}$ 且 $x_{0} \in\left(\dfrac{1}{3}, \dfrac{1}{2}\right)$．
2、令 $H(x)=\dfrac{f(x)}{x}$，求 $H(x)$ 的最小值．
已知函数 $y=a x \mathrm{e}^{x}$ 与 $y=\ln x+x$ 的图象有两个交点，则实数 $a$ 的取值范围为（ ）
A．$\left(0, \dfrac{1}{\mathrm{e}}\right)$
B．$\left(0, \dfrac{2}{\mathrm{e}}\right)$
C．$\left(-\infty, \dfrac{1}{\mathrm{e}}\right)$
D．$\left(-\infty, \dfrac{2}{\mathrm{e}}\right)$
关于函数 $f(x)=\dfrac{2\left(x^{3}-x\right)}{\mathrm{e}^{|x|}+x^{2}}$（$-10 \leqslant x \leqslant 10$），正确的描述有（ ）
A．是奇函数
B．是偶函数
C．有 $2$ 个极大值点
D．有 $3$ 个零点
已知圆 $C: x^{2}+y^{2}-8 x-4 y+19=0$，直线 $l: 3 x-2 y-6=0$，直线 $l$ 交圆 $C$ 于 $A, B$ 两点，设点 $P(2,0)$，则 $|P A| \cdot|P B|=$ （ ）
A．$\sqrt{3}$
B．$\sqrt{5}$
C．$5$
D．$7$
