1．已知数列$\{a_n\}$满足$a_1=1$，$a_{n+3}\leqslant a_n+3$，$a_{n+2}\geqslant a_n+2$，求$\{a_n\}$．
2．设点$P(x,y)$是曲线$a|x|+b|y|=1$($a>0,b>0$)上的动点，且始终满足$\sqrt{x^2+y^2+2y+1}+\sqrt{x^2+y^2-2y+1}\leqslant 2\sqrt 2$，则$a+\sqrt 2b$的取值范围是________．
3．已知$P$为椭圆$E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)上的动点，$F_1,F_2$为椭圆的两个焦点，设$\triangle PF_1F_2$的外接圆和内切圆半径分别为$R,r$，求$\dfrac{R}{r}$的取值范围．
4．已知$a,b,c$是$\triangle ABC$的三条边长，且$a^2+2b^2+3c^2=1$，求$\triangle ABC$面积的最大值．
5．已知集合$M=\{1,2,\cdots ,99\}$，现随机选取$M$中的$9$个元素，设$x$为这$9$个元素的中的最小数，求$x$的数学期望．
6．已知实数$a,b,c$和正实数$\lambda$使得$x^3+ax^2+bx+c=0$有三个实根$x_1,x_2,x_3$，且满足$x_2-x_1=\lambda$，$x_3>\dfrac{x_1+x_2}2$，求证：$\dfrac{2a^3+27c-9ab}{\lambda^3}\leqslant \dfrac{3\sqrt 3}2$．
7．已知$f(x)=x^2-2x+\sin\dfrac{\pi}2x$，$x\in (0,1)$．记$f(x)$的极小值点为$x_0$，若$f(x_1)=f(x_2)$，且$x_1<x_2$，求证：$x_1+x_2>2x_0$．
参考答案
1．对任意正整数$n$，均有$$\begin{cases} a_n+4\leqslant a_{n+4}\leqslant a_{n+1}+3,\\ a_n+9\geqslant a_{n+9}\geqslant a_{n+1}+8,\end{cases} $$于是$$a_{n+1}=a_n+1,$$从而$$a_n=n,n\in\mathcal N^*.$$
2．根据题意，有$$\sqrt{x^2+(y+1)^2}+\sqrt{x^2+(y-1)^2}\leqslant 2\sqrt 2,$$于是$P$点在以$F_1(0,-1)$，$F_2(0,1)$为焦点，$2\sqrt 2$为长轴长的椭圆$\dfrac{y^2}2+x^2=1$内部(包含边界)．而曲线$a|x|+b|y|=1$($a>0,b>0$)表示菱形$ABCD$，其中$A\left(\dfrac 1a,0\right)$，$B\left(0,\dfrac 1b\right)$，$C\left(-\dfrac 1a,0\right)$，$D\left(0,-\dfrac 1b\right)$．这样就有$$\dfrac 1a\leqslant 1,\dfrac 1b\leqslant \sqrt 2,$$于是$a+\sqrt 2b$的取值范围是$\left[2,+\infty\right)$．
3．设椭圆的焦距$|F_1F_2|=2c=2\sqrt{a^2-b^2}$，$\angle F_1PF_2=\theta$，则$$R=\dfrac{|F_1F_2|}{2\sin\theta}=\dfrac{c}{\sin\theta},$$下面计算内切圆半径$r$：
用面积计算有$$r=\dfrac{2S_{\triangle PF_1F_2}}{|PF_1|+|PF_2|+|F_1F_2|}=\dfrac{2b^2\tan\dfrac{\theta}2}{2a+2c}=(a-c)\tan{\dfrac{\theta}{2}},$$其中用到了焦点三角形的面积$S_{\triangle F_1PF_2}=b^2\tan\dfrac{\theta}2,\theta=\angle F_1PF_2$．
用内切圆的性质有$$r=\dfrac{2a-2c}{2}\cdot\tan{\dfrac{\theta}{2}}=(a-c)\tan\dfrac{\theta}{2}.$$
于是$$\dfrac{R}{r}=\dfrac{c}{2(a-c)}\cdot \dfrac{1}{\sin^2\dfrac{\theta}2},$$考虑到$\sin\dfrac{\theta}2$的取值范围是$\left(0,\dfrac ca\right]$，因此所求$\dfrac{R}{r}$的取值范围是$\left[\dfrac{a^2}{2(a-c)c},+\infty\right)$．
4．由三角形面积的三斜求积公式，有$\triangle ABC$的面积\[\begin{split} S&=\dfrac 14\sqrt{4b^2c^2-\left(b^2+c^2-a^2\right)^2}\\&=\dfrac 14\sqrt{4b^2c^2-\left(3b^2+4c^2-1\right)^2}\\&=\dfrac 14\sqrt{-9b^4-16c^4-20b^2c^2+6b^2+8c^2-1}\\&=\dfrac 14\sqrt{-\left(3b^2+\dfrac{10}3c^2-1\right)^2+\left(\dfrac{10}3c^2-1\right)^2-16c^4+8c^2-1}\\&=\dfrac 14\sqrt{-\left(3b^2+\dfrac{10}3c^2-1\right)^2-\dfrac{44}9\left(c^2-\dfrac 3{22}\right)^2+\dfrac{1}{11}}\\&\leqslant \dfrac{1}{4\sqrt{11}}=\dfrac{\sqrt{11}}{44},\end{split} \]等号当$c^2=\dfrac{3}{22}$，$b^2=\dfrac{2}{11}$，$a^2=\dfrac{5}{22}$时取得．于是$\triangle ABC$面积的最大值为$\dfrac{\sqrt{11}}{44}$．
5．根据题意，有\[\begin{split} E(x)&=\dfrac{1\cdot{\rm C}_{98}^8+2\cdot {\rm C}_{97}^8+3\cdot {\rm C}_{96}^8+\cdots +91\cdot {\rm C}_{8}^8}{{\rm C}_{99}^9}\\&=\dfrac{{\rm C}_{99}^9+1\cdot {\rm C}_{97}^8+2\cdot {\rm C}_{96}^8+\cdots +90\cdot {\rm C}_8^8}{{\rm C}_{99}^9}\\
&=\dfrac{{\rm C}_{99}^9+{\rm C}_{98}^9+1\cdot {\rm C}_{96}^8+\cdots +89\cdot{\rm C}_{8}^8}{{\rm C}_{99}^9}\\&=\cdots \\&=\dfrac{{\rm C}_{99}^9+{\rm C}_{98}^9+{\rm C}_{97}^9+\cdots +{\rm C}_{9}^9}{{\rm C}_{99}^9}\\
&=\dfrac{{\rm C}_{100}^{10}}{{\rm C}_{99}^9}\\&=10.\end{split} \]
注 本题中用到了组合数的性质$${\rm C}_{n}^{n}+{\rm C}_{n+1}^n+\cdots+{\rm C}_{n+k}^n={\rm C}_{n+k+1}^{n+1}.$$将${\rm C}_n^n$写成${\rm C}_{n+1}^{n+1}$，再利用组合数的性质${\rm C}_n^m+{\rm C}_{n}^{m-1}={\rm C}_{n+1}^m$即可证明．
6．根据题意，设$x_1=t\lambda$，$x_2=(1+t)\lambda$，$x_3=\left(t+\dfrac 12+m\right)\lambda$，由三次方程的韦达定理可得\[\begin{split} a&=-\left(x_1+x_2+x_3\right)=-\left(3t+\dfrac 32+m\right)\lambda,\\b&=x_1x_2+x_2x_3+x_3x_1=\left[3t^2+(3+2m)t+\dfrac 12+m\right]\lambda^{2},\\c&=-x_1x_2x_3=-\left[t^3+\left(\dfrac 32+m\right)t^2+\left(\dfrac 12+m\right)t\right]\lambda^{3},\end{split} \]于是$$\dfrac{2a^3+27c-9ab}{\lambda^3}=-2m^3+\dfrac 92m=\dfrac{1}{2}\cdot \sqrt{4m^2\cdot\left(\dfrac 92-2m^2\right)\cdot\left(\dfrac 92-2m^2\right)}\leqslant \dfrac12\sqrt{3^{3}}=\dfrac 32\sqrt 3,$$当$m^{2}=\dfrac 34$时等号成立，原命题得证．
注 最后一步均值不等式得到的结果也可以通过函数求导的方式得到．
7．根据题意，有$f(x)$的导函数$$f'(x)=2x-2+\dfrac{\pi}2\cos\dfrac{\pi}2x,$$其二阶导函数$$f''(x)=2-\dfrac{\pi^2}4\sin\dfrac{\pi}2x.$$构造二次函数$$g(x)=\dfrac 12f''(x_0)(x-x_0)^2+f(x_0),$$记$h(x)=f(x)-g(x)$，则$$h''(x)=f''(x)-f''(x_0),$$结合$f''(x)$单调递减，可得在$(0,x_0)$上$h''(x)>0$，在$(x_0,1)$上$h''(x)<0$．进而由$h'(x)=f'(x)-g'(x)$可得$h'(x_0)=f'(x_0)=0$，从而在区间$(0,1)$上均有$h'(x)\leqslant 0$．这样再结合$h(x_0)=0$，可得在区间$(0,x_0)$上$h(x)>0$，在区间$(x_0,1)$上$h(x)<0$，因此函数$f(x)$和$g(x)$的图象如图所示．
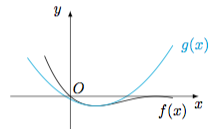设$f(x_1)=f(x_2)=g(x_3)=g(x_4)$($x_3<x_4$)，这样我们就有$$x_3<x_1<x_0<x_4<x_2,$$从而$$x_1+x_2>x_3+x_4=2x_0,$$原命题得证．