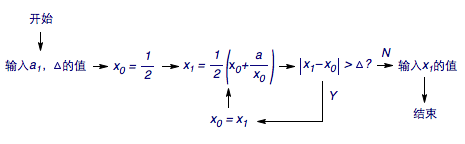1、已知圆$O:x^2+y^2=1$.若直线$y=kx+2$上总存在点$P$,使得过点$P$的圆$O$的两条切线互相垂直,则实数$k$的取值范围是_______.
2、已知曲线$C:\sqrt{2x+y-\sqrt 2}\cdot\sqrt{4x^2+y^2-2}=0$,对于下列命题:
① 曲线$C$为轴对称图形;
② 曲线$C$与坐标轴围成封闭图形的面积小于$\dfrac{\pi}2$;
③ 曲线$C$上的点到原点的距离最小值为$\dfrac{\sqrt{10}}5$;
④ 已知点$A\left(0,-\dfrac{\sqrt 6}2\right)$,$B\left(0,\dfrac{\sqrt 6}{2}\right)$,$P$为曲线$C$上一点,则有$PA+PB\geqslant 2\sqrt 2$.
上述命题中,真命题的序号是_______.
3、某商场对顾客实行购物优惠活动,规定一次性购物付款规则如下:
① 如果一次性购物不超过200元,则不给予优惠;
② 如果一次性购物超过200元,但不超过500元,则按标价给予9折优惠;
③ 如果一次性购物超过500元,则500元按第②条给予优惠,剩余部分给予7折优惠.
甲单独购买A商品实际付款100元,乙单独购买B商品,实际付款450元,若丙一次性购买A、B两件商品,则应付款_______元.
4、设函数\[f(x)=\begin{cases}|x-a|,&x\leqslant 1,\\{\log_2}x,&x>1.\end{cases}\]
(1)如果$f(1)=3$,那么实数$a=$_______;
(2)如果函数$y=f(x)-2$有且仅有两个零点,那么实数$a$的取值范围是_______.
5、已知两点$M(-1,0)$,$N(1,0)$,若直线$y=k(x-2)$上至少存在三个点$P$,使得三角形$MNP$是直角三角形,则实数$k$的取值范围是_______.
6、阅读下面的框图,回答问题:
(1)若输入$a=1$,$\Delta=0.1$,则输出的$x_1=$_______;
(2)如输入$a=2$,则对输入$\forall\Delta >0$,均有输出的$x_1$满足:
① $N<x_1$;② $x_1\leqslant M$.
选定你认为正确的结论_______,指出$N$或$M$的取值范围________.
7、已知数集$A=\left\{a_1,a_2,a_3,a_4,a_5\right\}$,其中$0\leqslant a_1<a_2<a_3<a_4<a_5$,具有性质:
对于任意$i,j\in\mathcal N$,其中$1\leqslant i\leqslant j \leqslant 5$,$a_j+a_i$与$a_j-a_i$中至少有一个属于$A$.
若$a_5=60$,则$a_1=$_______;$a_3=$_______.
参考答案
1、$(-\infty ,-1]\cup [1,+\infty )$
2、②④
3、520
4、(1)$4$或$-2$;(2)$(-1,3]$
5、$\left[-\dfrac{\sqrt 3}3,0\right)\cup\left(0,\dfrac{\sqrt 3}3\right]$
6、(1)$\dfrac{3281}{3280}$;(2)①②均正确;$N\leqslant\sqrt 2$,$M\geqslant\dfrac{9}{4}$.
7、$0$;$30$