每日一题[5] 椭圆的光学性质

  证明：从椭圆焦点出发的光线，经过椭圆反射后反射光线必经过另一个焦点．

---

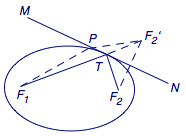
如图，设反射点为$T$，反射面为$MN$，我们只需要证明若$\angle MTF_1=\angle NTF_2$，那么$MN$为切线．

显然$MN$上的点$T$在椭圆上，我们只需要证明直线$MN$上不存在椭圆上除$T$以外的其他点．

用反证法，假设直线$MN$上存在除$T$以外的椭圆上的点$P$，则$PF_1+PF_2=2a$（椭圆定义）．

作$F_2$关于$MN$对称的点$F_2'$，则$F_1$、$T$、$F_2'$共线，于是

$$F_1F_2'=F_1T+TF_2=2a.$$

于是$PF_1+PF_2'>F_1F_2'=2a$（三角形两边之和大于第三边），矛盾．

因此直线$MN$上不存在除$T$以外的椭圆上的点，也即直线$MN$与椭圆相切．