每日一题[88] 抛物线的光学性质

（2015年北京市东城区高三一模数学理科）在平面直角坐标系$xOy$中，动点$E$到定点$(1,0)$的距离与它到直线$x=-1$的距离相等．

（1）求动点$E$的轨迹$C$的方程；

（2）设动直线$l:y=kx+b$与曲线$C$相切于点$P$，与直线$x=-1$相交于点$Q$．证明：以$PQ$为直径的圆恒过$x$轴上的某定点．

---

（1）解    根据抛物线的定义可知动点$E$的轨迹为抛物线，其方程为

$$C:y^2=4x.$$

（2）解   以$PQ$为直径的圆恒过抛物线$C$的焦点$F(1,0)$，证明如下．

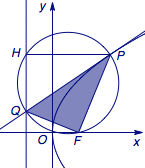过$P$作准线$x=-1$的垂线，垂足为$H$．由抛物线的光学性质有

$$\angle FPQ=\angle QPH,$$ 根据抛物线的定义有 $$PF=PH,$$ 因此三角形$PQF$与三角形$PQH$全等，于是$\angle PFQ$恒为直角，进而以$PQ$为直径的圆恒过抛物线$C$的焦点$F(1,0)$．

---

注    抛物线的光学性质的证明可以仿照椭圆的光学性质的证明进行，留给读者．