每日一题[2] 二次曲线上的四点共圆

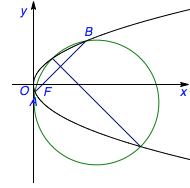
已知抛物线\(y^2=2px(p>0)\)，\(AB\)为过抛物线焦点\(F\)的弦，\(AB\)的中垂线交抛物线\(E\)于点\(M\)、\(N\)．若\(A\)、\(M\)、\(B\)、\(N\)四点共圆，求直线\(AB\)的方程．

设圆的两条弦所在直线的交点为\(P(x_0,y_0)\)，过\(P\)的直线

\[l:\begin{cases}x=x_0+t,\\y=y_0+kt,\end{cases}\]

则与抛物线联立可得

\[(y_0+kt)^2=2p(x_0+t),\]

整理得\[k^2t^2+(2y_0k-2p)t+y_0^2-2px_0=0.\]

于是\[t_1t_2=\frac{y_0^2-2px_0}{k^2}.\]

因此\(k_{AB}=-k_{MN}\)．

结合本题已知\(AB\perp MN\)，于是\[k_{AB}=\pm 1.\]

因此直线\(AB\)的方程为\[y=\pm x\mp \frac p2.\]

注一    事实上，本题中\(k_{AB}=-k_{MN}\)的结论可以推广到对任意二次曲线都成立．

注二    本题与2014年全国高中数学联赛河南省预赛第10题基本相同．

2015年8月11日补充练习题：

（2014年全国高中数学联赛湖北省预赛第12题）设\(A\)、\(B\)是双曲线\(x^2-\dfrac{y^2}{2}=\lambda\)上的两点，点\(N(1,2)\)是线段\(AB\)的中点，线段\(AB\)的垂直平分线交双曲线于\(C\)、\(D\)两点．

（1）确定\(\lambda\)的取值范围；

（2）试判断\(A,B,C,D\)是否四点共圆？并说明理由．