每日一题[182] 迭代函数法

2015年北京市人大附中高二期末考试压轴题：

数列\(\{a_n\}\)满足：\(a_{n+1}=3a_n-3a_n^2\)，\(n=1,2,3,\cdots\)．

（1）若数列\(\{a_n\}\)为常数列，求\(a_1\)的值；

（2）若\(a_1=\dfrac 12\)，求证：\(\dfrac 23<a_{2n}\leqslant \dfrac 34\)；

（3）在（2）的条件下，求证：数列\(\{a_{2n}\}\)单调递减．

（1）解    解不动点方程\[x=3x-3x^2,\]得\[x=0\lor x=\dfrac 23.\]于是\(a_1\)的值为\(0\)或\(\dfrac 23\)．

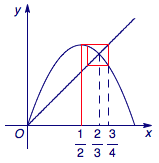
（2）证明    如图，将命题加强为\[\begin{cases}\dfrac 12\leqslant a_{2n-1} < \dfrac 23,\\\dfrac 23<a_{2n}\leqslant \dfrac 34.\end{cases}\]下面用数学归纳法证明．

当\(n=1\)时，显然有\(\dfrac 12\leqslant a_1<\dfrac 23\)且\(\dfrac 23<a_2\leqslant \dfrac 34\)；

假设命题对\(n\)成立，则由于函数\(f(x)=3x-3x^2\)在区间\(\left[\dfrac 12,\dfrac 34\right]\)上单调递减，于是\[f\left(\dfrac 23\right)>f\left(a_{2n}\right)\geqslant f\left(\dfrac 34\right),\]即\[\dfrac{9}{16}\leqslant a_{2n+1}<\dfrac 23,\]从而\[\dfrac 12\leqslant a_{2n+1}<\dfrac 23.\]再次利用函数\(f(x)\)的单调性可得\[f\left(\dfrac 12\right) \geqslant f\left(a_{2n+1}\right) > f\left(\dfrac 23\right),\]即\[\dfrac 23<a_{2n+2}\leqslant \dfrac 34,\]于是命题对\(n+1\)也成立．

综上，命题得证．

（3）证明   与（2）类似，将命题加强为数列\(\{a_{2n-1}\}\)单调递增，且数列\(\{a_{2n}\}\)单调递减．

根据已知，\(a_1=\dfrac 12\)，\(a_2=\dfrac 34\)，\(a_3=\dfrac 9{16}\)，于是\[a_1<a_3\Rightarrow f(a_1)>f(a_3)\Rightarrow a_2>a_4,\]于是归纳基础得证．

假设命题对\(n\)成立，即\(a_{2n-1}<a_{2n+1}\)，且\(a_{2n}>a_{2n+2}\)，则有\[f\left(a_{2n}\right)<f\left(a_{2n+2}\right)\Rightarrow a_{2n+1}< a_{2n+3},\]进而\[f\left(a_{2n+1}\right)>f\left(a_{2n+3}\right) \Rightarrow a_{2n+2}>a_{2n+4},\]于是命题对\(n+1\)也成立．

综上，命题得证．

注    菁优网给出的解答：

http://www.jyeoo.com/math2/ques/detail/d5df81c5-408c-4a73-9c52-790e10e87c73