每日一题[172] 三角形的面积与高

2015年高考上海卷理科数学第14题（填空题压轴）：

在锐角三角形$ABC$中，$\tan A=\dfrac 12$，$D$为$BC$上的点，$\triangle ABD$与$\triangle ACD$的面积分别为$2$和$4$，过$D$作$DE\perp AB$于$E$，$DF\perp AC$于$F$，则$\overrightarrow{DE}\cdot \overrightarrow{DF}=$_______．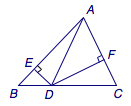

---

正确答案是$-\dfrac{16}{15}$．

注意到$\overrightarrow{DE}$和$\overrightarrow{DF}$的夹角为$\pi-A$，因此问题的关键在于求$DE\cdot DF$，而$DE$、$DF$的“身份”分别为$\triangle ABD$和$\triangle ADC$的高，因此有

$$\begin{split}\overrightarrow{DE}\cdot \overrightarrow{DF}&=DE\cdot DF\cdot\cos (\pi -A)\\&=\dfrac{2\triangle ABD}{AB}\cdot\dfrac{2\triangle ADC}{AC}\cdot\left(-\dfrac{2}{\sqrt 5}\right)\\&=-\dfrac{64}{\sqrt 5}\cdot \dfrac{1}{AB\cdot AC}\\&=-\dfrac{64}{\sqrt 5}\cdot \dfrac{\triangle ABC}{6 \cdot AB\cdot AC}\\&=-\dfrac{64}{\sqrt 5}\cdot \dfrac{\dfrac 12\sin A}{6}\\&=-\dfrac{16}{15}.\end{split}$$