已知 $f(x)=\sin \omega x-\cos \omega x$，其中 $\omega >\dfrac 14$，$x\in\mathbb R$，若 $f(x)$ 的任何一条对称轴与 $x$ 轴交点的横坐标都不属于区间 $(2\pi ,3\pi)$，则 $\omega$ 的取值范围是（ ）
A．$\left[\dfrac 38,\dfrac{11}{12}\right]\cup\left[\dfrac{11}8,\dfrac{19}{12}\right]$
B．$\left(\dfrac 14,\dfrac{5}{12}\right]\cup\left[\dfrac{5}8,\dfrac{3}{4}\right]$
C．$\left[\dfrac 38,\dfrac{7}{12}\right]\cup\left[\dfrac{7}8,\dfrac{11}{12}\right]$
D．$\left(\dfrac 14,\dfrac{3}{4}\right]\cup\left[\dfrac{9}8,\dfrac{17}{12}\right]$
正确答案是C．
分析与解 根据题意，有\[f(x)=\sqrt 2\sin \left(\omega x-\dfrac{\pi}4\right),\]接下来考虑问题的反面，也即\[\exists k\in\mathbb Z,2\omega\pi-\dfrac{\pi}4<k\pi+\dfrac{\pi}2<3\omega\pi-\dfrac{\pi}4,\]也即\[\exists k\in \mathbb Z,\dfrac 13k +\dfrac 14<\omega <\dfrac 12k+\dfrac 38.\]如图．
因此所求 $\omega$ 的取值范围是 $\left[\dfrac 38,\dfrac{7}{12}\right]\cup\left[\dfrac{7}8,\dfrac{11}{12}\right]$．
其它解法 可以结合图象，从图象伸缩角度得到取值范围．示意图如下：
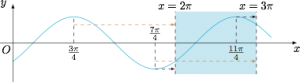注 也可以不考虑问题的反面，$f(x)$ 的对称轴\[x=\dfrac{k+\frac 34}{\omega}\pi\notin(2\pi,3\pi),\]即\[\forall k\in\mathbb{Z},\left(\omega\geqslant \dfrac k2+\dfrac 38\right) \lor\left(\omega\leqslant\dfrac k3+\dfrac 14\right),\]记\[A_k=\left\{\omega\mid\omega\leqslant\dfrac k3+\dfrac 14 \lor \omega\geqslant \dfrac k2+\dfrac 38\right\},\]因为 $\dfrac{2\pi}{\omega}\geqslant 2\pi$，所以\[\omega\in\left(\dfrac 14,1\right].\]从而只需要考虑 $k=0,1,2$ 即可，得到 $\omega$ 的取值范围是\[A_0\cap A_1\cap A_2=\left[\dfrac 38,\dfrac 7{12}\right]\cup\left[\dfrac 78,\dfrac{11}{12}\right].\]