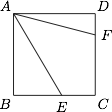
已知正方形 $ABCD$ 的边长为 $1$，点 $E,F$ 分别在边 $BC$ 与 $CD$ 上（包含端点），且 $\angle EAF=45^\circ$，则 $\sqrt{BE^2+DF^2}$ 的取值范围是 ______．
正确答案是$\left[2-\sqrt 2,1\right]$．
分析与解 如图，将 $\triangle ADF$ 旋转到 $\triangle ABG$，则 $\triangle AGE$ 与 $\triangle AFE$ 全等．
因此题中条件转化为 $BE,DF\in [0,1]$，且\[(1-BE)^2+(1-DF)^2=(BE+DF)^2,\]也即\[BE+DE+BE\cdot DF=1,\]于是\[1\leqslant 2\cdot \sqrt{\dfrac{BE^2+DF^2}2}+\dfrac{BE^2+DF^2}2,\]解得\[\sqrt{BE^2+DF^2}\geqslant 2-\sqrt 2,\]等号当 $BE=DF=\sqrt 2-1$ 时取得．因此 $\sqrt{BE^2+DF^2}$ 的最小值为 $2-\sqrt 2$．
另一方面，有\[\sqrt{BE^2+DF^2}\leqslant BE+DF \leqslant 1,\]等号当 $BE=0$ 或 $DF=0$ 时取得．因此 $\sqrt{BE^2+DF^2}$ 的最大值为 $1$．
结合连续性可知所求代数式的取值范围是 $\left[2-\sqrt 2,1\right]$．
注 本题也可以设角度，利用三角函数知识求解，但计算量较大．
