点 \(P(x,y)\) 是曲线 \(C:y=\dfrac 1x\)（\(x>0\)）上的一个动点，曲线 \(C\) 在点 \(P\) 处的切线与 \(x\) 轴、\(y\) 轴分别交于 \(A,B\) 两点，点 \(O\) 是坐标原点，则（ ）
A．\(|PA|=|PB|\)
B．\(\triangle OAB\) 的面积为定值
C．曲线 \(C\) 上存在两点 \(M,N\) 使得 \(\triangle OMN\) 是等边三角形
D．曲线 \(C\) 上存在两点 \(M,N\) 使得 \(\triangle OMN\) 是等腰直角三角形
正确答案是ABCD．
分析与解 选项A 先证明一个引理．
引理 若直线 \(l\) 是曲线 \(C:y=\dfrac 1x\) 的割线，且割点分别为 \(P,Q\)，直线 \(l\) 与 \(x\) 轴、\(y\) 轴分别交于 \(A,B\) 两点，则 \(PB=QA\)，如图．
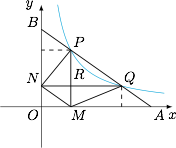证明 过 \(P,Q\) 作两坐标轴的垂线，设 \(PM\) 与 \(x\) 轴垂直且相交于 \(M\)，\(QN\) 与 \(y\) 轴垂直且相交于 \(N\)，\(PM\) 与 \(QN\) 相交于 \(R\)，则根据反比例函数图象的性质，有 \(S_{\triangle NPR}=S_{\triangle MQR}\)，因此\[S_{\triangle NPQ}=S_{\triangle MPQ},\]进而 \(MN\parallel PQ\)，从而 \(BP,NM,QA\) 平行且相等，于是引理得证．
根据引理，当 \(P,Q\) 重合时，割线变成切线，此时有 \(|PA|=|PB|\)，命题成立．
选项B 由于 \(|PA|=|PB|\)，因此 \(\triangle OAB\) 的面积为定值 \(2\)．
选项C 在曲线 \(C\) 上选取关于 \(y=x\) 对称的两点 \(M,N\)，形成等腰 \(\triangle OMN\)，当 \(N\) 从 \((1,0)\) 向 \((+\infty,0)\) 运动时，\(\triangle OMN\) 的顶角 \(\angle MON\) 从 \(0\) 增大到 \(90^\circ\)，在运动的过程中必然存在 \(\triangle MON\) 为 \(60^\circ\) 的时刻，此时 \(\triangle MON\) 为等边三角形，命题正确．
选项D 过 \(O\) 作射线 \(OM\)，与曲线 \(C\) 交于 \(M\)．将射线 \(OM\) 顺时针旋转 \(45^\circ\) 得到射线 \(ON\)，与曲线 \(C\) 交于 \(N\)．当 \(M\) 从 \((0,+\infty)\) 运动到 \((1,1)\) 时，\( \dfrac{OM}{ON} \) 的值从 \( +\infty \) 变化到 \( 0 \)，在运动的过程中必然存在 \( \dfrac{OM}{ON} \) 为 \( \sqrt 2 \) 和 \( \dfrac{\sqrt 2}2 \) 的时刻，此时 \( \triangle MON \) 为等腰直角三角形，命题正确．
注 选项A，B也可以直接求出切线方程判断真假．