每日一题[107] 调整法解最值问题

设函数$f(x)=\left|ax+b-\sqrt x\right|,x\in [0,4]$，其中$a,b$为实数．设$f(x)$的最大值为$M(a,b)$，求$M(a,b)$的最小值．

正确答案是$\dfrac{1}{4}$．

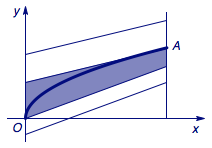
记$O(0,0)$，$A(4,2)$，抛物线段$E:y=\sqrt x,x\in [0,4]$．

首先，任意一条与抛物线段$E$无公共点的线段，都可以通过平移使其与抛物线段$E$有公共点，并在此过程中$M(a,b)$变小，如图．

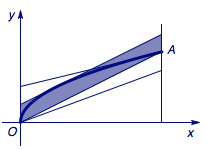
接下来，将与抛物线段$E$有公共点的线段的斜率调整到$\dfrac{1}{2}$，在调整过程中，$M(a,b)$变小或不变，如图．

最后，在斜率为$\dfrac{1}{2}$，且位于抛物线段$E$的切线（$y=\dfrac 12x+\dfrac 12$）和割线（$y=\dfrac 12x$）之间的线段中，位于居中位置的$y=\dfrac 12x+\dfrac 14$使得$M(a,b)$最小，此时$M(a,b)$的最小值为$\dfrac{1}{4}$．