已知 \(\triangle ABC\) 的面积为 \(1\)，\(AB\) 的平行线分别交 \(AC,BC\) 于 \(D,E\)，连接 \(BD\)，\(\triangle DCE,\triangle DBE,\triangle DBA\) 的面积分别记为 \(S_1,S_2,S_3\)，则（ ）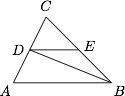
A．\(\max\{S_1,S_2,S_3\}\) 的最小值为\(\dfrac 13\)
B．\(\max\{S_1,S_2,S_3\}\) 的最小值为\(\dfrac{3-\sqrt 5}2\)
C．\(\min\{S_1,S_2,S_3\}\) 的最大值为\(\dfrac 13\)
D．\(\min\{S_1,S_2,S_3\}\) 的最大值为\(\dfrac 14\)
注 所有选择题默认是不定项选择．
正确答案是BD．
分析与解 设 \(\dfrac{CD}{CA}=\dfrac{CE}{CB}=x\)，\(x\in(0,1)\)，则\[\begin{split}S_1(x)&=x^2,\\S_2(x)&=x-x^2,\\S_3(x)&=1-x.\end{split}\]如图，\(P\) 点为函数 \(S_1(x)\) 与函数 \(S_3(x)\) 图象的公共点，\(Q\) 点为函数 \(S_1(x)\) 与函数 \(S_2(x)\) 图象的公共点，它们的坐标分别为\[P\left(\dfrac{\sqrt 5-1}2,\dfrac{3-\sqrt 5}2\right),Q\left(\dfrac 12,\dfrac 14\right).\]