每日一题[1043]透视原理的应用

用一个平面去截正四面体，使它成为形状、大小都相同的两个几何体，则这样的平面个数为（　　）

A．\(6\)
B．\(7\)
C．\(10\)
D．无数

正确答案是D．

分析与解　过对棱中点的平面均满足要求．
如图，$M,N$ 分别是棱 $AB,CD$ 的中点，对于过 $M,N$ 的任一截面 $MPNQ$，由透视原理可以得到$$\dfrac{AP}{DP}=\dfrac{BQ}{CQ},$$从而有$$AP=BQ,DP=QC.$$依次看各棱与各面的角，可以得到平面 $MPNQ$ 将正四面体分成的两部分完全相同，而过 $M,N$ 的平面有无数个．

更进一步，只需要$AM=DN$，过$M,N$的截面就可以满足要求．

透视原理　对于四面体$ABCD$，点$M,N,P,Q$分别是棱$AB,CD,AD,BC$上的点，若$\dfrac{AM}{MB}\cdot\dfrac{CN}{ND}=1$，且$\dfrac{DP}{PA}\cdot\dfrac{BQ}{QC}=1$，则直线$MP,QN,BD$三线共点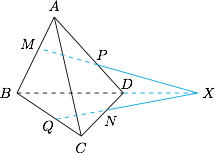．证明　设$MP\cap BD=X$，在$\triangle ABD$中用梅涅劳斯定理有$$\dfrac{AM}{MB}\cdot\dfrac{BX}{XD}\cdot\dfrac{DP}{PA}=1.$$设$QN\cap BD=X'$，在$\triangle BCD$中用梅涅劳斯定理有$$\dfrac{CN}{ND}\cdot\dfrac{DX'}{X’B}\cdot\dfrac{BQ}{QC}=1.$$两式两边分别相乘得到$$\dfrac{BX}{XD}\cdot\dfrac{DX'}{X'B}=1.$$所以$X$与$X'$重合，命题得证．