一张长方形白纸$ABCD$，其中$AD=1$，$AB=a$($a\geqslant 1$)．设$D_1$是边$AB$上一点，记$AD_1=x$．现拿起白纸的顶点$D$，将点$D$折向$D_1$，并保证端点$D$与$D_1$重合．设折后得到的图形中，不在原来的长方形$ABCD$范围的部分面积为$S$．
(1) 用$a$和$x$表示$S$；
(2) 当$a=1$时，在$D_1$点从$A$移动到$B$的过程中，求$S$的最大值．
分析与解 (1) 以$A$为原点，$AB$为$x$轴正方向建立平面直角坐标系，设$D_1(m,0)$，则折痕$$l:y=m\left(x-\dfrac m2\right)+\dfrac 12.$$
情形一 折痕与$AD,BC$相交，如图．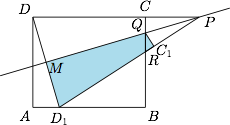
可以计算得\[P\left(\dfrac m2+\dfrac 1{2m},1\right),Q\left(a,am-\dfrac 12m^2+\dfrac 12\right),R\left(a,\dfrac{2m(a-m)}{1-m^2}\right),\]于是\[S=\dfrac 12(QR-QC)\cdot PC=\dfrac{m(m^2-2am+1)^2}{4(1-m^2)}.\]
情形二 折痕与$AD,CD$相交，此时$S=0$．
情形三 折痕与$AB,CD$相交，如图．
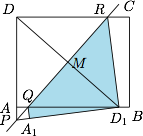可以计算得\[P\left(0,-\dfrac 12m^2+\dfrac 12\right),Q\left(\dfrac 12m-\dfrac{1}{2m},0\right),\]于是\[S=\dfrac 12(QD_1-QA)\cdot PA=\dfrac{m^2-1}{4m}.\]
综上所述，有\[S(x)=\begin{cases}\dfrac{x(x^2-2ax+1)^2}{4(1-x^2)},&x\in \left[0,a-\sqrt{a^2-1}\right],\\0,&x\in \left(a-\sqrt{a^2-1},1\right),\\\dfrac{x^2-1}{4x},&x\in [1,a].\end{cases}\]
(2) 当$a=1$时，有\[S(x)=\dfrac{x(1-x)^3}{4(x+1)},x\in [0,1].\]其导函数\[S'(x)=-\dfrac{(x-1)^2}{4(x+1)^2}\cdot (3x^2+4x-1),\]于是当$x=\dfrac{-2+\sqrt 7}3$时，$S(x)$取得极大值，亦为最大值\[S\left(\dfrac{-2+\sqrt 7}3\right)=\dfrac{316-119\sqrt{7}}{54}.\]