每日一题[997]用解析办法解平几问题

已知矩形$ABCD$中$AB=\sqrt 2BC$，以$CD$为直径向矩形外作半圆，设$P$为半圆上任意一点，直线$PA,PB$分别与$CD$相交于点$M,N$，求证：$CD^2=CM^2+DN^2$．

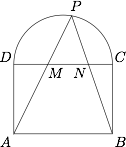
证明　以$CD$的中点为原点，$DC$为$x$轴方向建立平面直角坐标系，不妨设$AB=2$，如图．
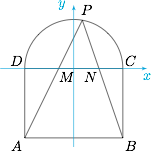设$P(\cos\theta,\sin\theta)$，$A(-1,-\sqrt 2)$，$B(1,-\sqrt 2)$，$C(1,0)$，$D(-1,0)$，于是根据截距坐标公式，$M,N$的横坐标分别为\[\begin{split}
x_M&=\dfrac{\cos\theta\cdot (-\sqrt 2)-(-1)\cdot \sin\theta}{-\sqrt 2-\sin\theta}\\&=\dfrac{-\sin\theta+\sqrt 2\cos\theta}{\sqrt 2+\sin\theta},\\x_N&=\dfrac{\cos\theta\cdot (-\sqrt 2)-1\cdot \sin\theta}{-\sqrt 2-\sin\theta}\\&=\dfrac{\sin\theta+\sqrt 2\cos\theta}{\sqrt 2+\sin\theta},\end{split}\]于是\[\begin{split}CM^2+DN^2&=\left(1-x_M\right)^2+\left(x_N-(-1)\right)^2\\&=\dfrac{\left(\sqrt 2+2\sin\theta-\sqrt 2\cos\theta\right)^2+\left(\sqrt 2+2\sin\theta+\sqrt 2\cos\theta\right)^2}{\left(\sqrt 2+\sin\theta\right)^2}\\&=4=CD^2,\end{split}\]因此原命题得证．